
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像相交于A(
的图像相交于A(![]() )、B(
)、B(![]() )两点。
)两点。
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)根据图像直接写出使一次函数的值大于反比例函数的值的![]() 的取值范围
的取值范围
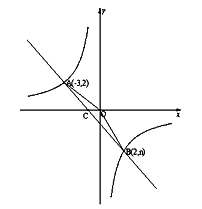
【答案】(1)反比例函数的解析式为y=![]() ,一次函数的解析式为y=-x-1;(2)C(-1,0),面积为
,一次函数的解析式为y=-x-1;(2)C(-1,0),面积为![]() ;(3)当x<-3或0<x<2时,一次函数值大于反比例函数值
;(3)当x<-3或0<x<2时,一次函数值大于反比例函数值
【解析】
(1)根据待定系数法,可得反比例函数解析式,根据B在函数图象上,可得B点的坐标,根据待定系数法,可得一次函数的解析式;
(2)根据一次函数的纵坐标为0,可得点C的坐标,根据S△AOB=S△AOC+S△BOC可得答案;
(3)根据观察图象,一次函数图象在上的区域对应x的范围即可.
(1)把A(-3,2)代入y=![]() 得m=-6
得m=-6
∴反比例函数的解析式为y=![]() ,
,
又∵B(2,n)在反比例图象上,得n=-3,
∴B(2,-3)
把A(-3,2)和B(2,-3)代入y=kx+b中得:
![]() 解得
解得![]() ,
,
∴一次函数的解析式为y=-x-1;
(2)当y=0时,y=-x-1得x=-1,
∴y=-x-1与x轴的交点坐标是 C(-1,0),
S△AOB=S△AOC+S△BOC
=![]() ×|1|×2+
×|1|×2+![]() ×|1|×|3|
×|1|×|3|
=![]() ;
;
(3)当x<-3或0<x<2时,一次函数值大于反比例函数值.


科目:初中数学 来源: 题型:
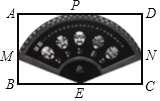
【题目】在一张矩形纸片ABCD上制作一幅扇形艺术画.扇形的圆弧和边AD相切,切点为P,BC边中点E为扇形的圆心,半径端点M,N分别在边AB,CD上,已知AB=10cm,BC=10![]() cm,则扇形艺术画的面积为_____.
cm,则扇形艺术画的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以![]() 米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为
米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为![]() (米)与时间
(米)与时间![]() (分钟)的关系如图.请结合图象,解答下列问题:
(分钟)的关系如图.请结合图象,解答下列问题:

(1)填空:![]() ______;
______;![]() ______;
______;![]() ______.
______.
(2)求线段![]() 所在直线的解析式.
所在直线的解析式.
(3)若小军的速度是120米/分,求小军第二次与爸爸相遇时距图书馆的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
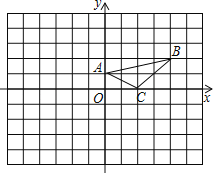
【题目】如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).
(1)将△ABC沿y轴翻折得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕着点(﹣1,﹣1)旋转180°得到△A2B2C2,画出△A2B2C2;
(3)线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(1)第1个等式:a1=![]() ; 第2个等式:a2=
; 第2个等式:a2=![]() ;
;
第3个等式:a3=![]() ; 第4个等式:a4=
; 第4个等式:a4=![]() ;
;
…
用含有n的代数式表示第n个等式:an=___________=___________(n为正整数);
(2)按一定规律排列的一列数依次为![]() ,1,
,1, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…,按此规律,这列数中的第100个数是_______________.
,…,按此规律,这列数中的第100个数是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某区八年级学生的睡眠情况,随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人,利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表(单位:小时)
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
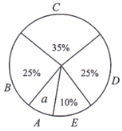
根据图表提供的信息,回答下列问题:
(1)试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数;
(2)如果睡眠时间x(时)满足:![]() ,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
,称睡眠时间合格.已知该区八年级学生有3250人,试估计该区八年级学生睡眠时间合格的共有多少人?
(3)如果将各组别学生睡眠情况分组的最小值(如C组别中,取![]() ),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
),B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两把不同的锁和四把不同的钥匙,其中两把钥匙恰好分别能打开这两把锁,其余的钥匙不能打开这两把锁.现在任意取出一把钥匙去开任意一把锁.
(1)请用列表或画树状图的方法表示出上述试验所有可能结果;
(2)求一次打开锁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M、N分别是射线CB和射线DC上的动点,且始终∠MAN=45°.
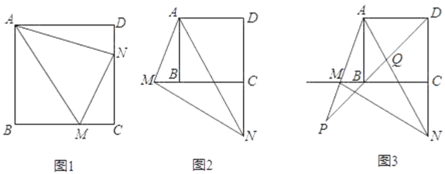
(1)如图1,当点M、N分别在线段BC、DC上时,请直接写出线段BM、MN、DN之间的数量关系;
(2)如图2,当点M、N分别在CB、DC的延长线上时,(1)中的结论是否仍然成立,若成立,给予证明,若不成立,写出正确的结论,并证明;
(3)如图3,当点M、N分别在CB、DC的延长线上时,若CN=CD=6,设BD与AM的延长线交于点P,交AN于Q,直接写出AQ、AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com