Question

16．如图，直线l₁：y=x+3与x轴交于点A，与y轴交于点P，直线l₂：y=-2x+m与x轴交于点B，与y轴交于点Q，l₁、l₂交于点R．
（1）当m=3时，△RAB的面积为$\frac{27}{4}$．（直接写出答案）
（2）当m≠3时，求△RAB的面积．（用含m的代数式表示）
（3）是否存在m，使△RQP的面积是△RAB的面积的2倍？若存在，求m的值；若不存在，请说明理由．

Answer 1

分析 （1）直线l₁：y=x+3与x轴交于点A，与y轴交于点P，令y=0，求得x=-3，令x=0，求得y=3，得到A、P的坐标将直线l₁：y=x+3和直线l₂：y=-2x+3联立组成有关x、y的方程组，利用三角形的面积公式计算即可；
（2）直线l₁：y=x+3与x轴交于点A，与y轴交于点B，令y=0，求得x=-3，令x=0，求得y=3，得到A、B的坐标将直线l₁：y=x+3和直线l₂：y=-2x+m联立组成有关x、y的方程组，利用三角形的面积公式计算即可；
（3）利用三角形的面积公式计算即可．

解答 解：（1）∵直线l₁：y=x+3与x轴交于点A，与y轴交于点P，
∴令y=0，求得x=-3，令x=0，求得y=3，
∴A（-3，0）、P（0，3），
∵直线l₁：y=-2x+3与x轴交于点B，
∴令y=0，求得x=1.5，
∴B（1.5，0）、
∵直线l₁与直线l₂y=-2x+3交于点R．
∴解$\left\{\begin{array}{l}{y=x+3}\\{y=-2x+3}\end{array}\right.$，
得$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$，
∴△RAB的面积为=$\frac{1}{2}×3×\frac{9}{2}=\frac{27}{4}$；
故答案为：$\frac{27}{4}$．
（2）直线l₂与x轴交点B（$\frac{m}{2}$，0），与y轴交点Q（0，m），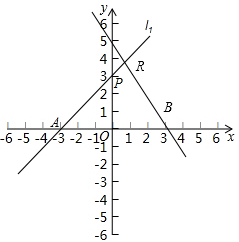

直线l₁与x轴交点A（-3，0），与y轴交点P（0，3），
由题意$\left\{\begin{array}{l}{y=x+3}\\{y=-2x+m}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=\frac{m-3}{3}}\\{y=\frac{m+6}{3}}\end{array}\right.$，
所以两条直线的交点R（$\frac{m-3}{3}，\frac{m+6}{3}$），
${S}_{△RAB}=\frac{1}{2}AB•RM=\frac{1}{2}•|\frac{m}{2}+3|•|\frac{m+6}{3}|$=$\frac{1}{12}{m}^{2}+m+3$；
（3）${S}_{△RPQ}=\frac{1}{2}×|m-3|×|\frac{m-3}{3}|=\frac{1}{6}（m-3）^{2}$，
∵S_△RPQ=2S_△RAB，
∴$\frac{1}{6}（m-3）^{2}=（\frac{1}{12}{m}^{2}+m+3）×2$，
解得：m=-$\frac{3}{2}$．

点评 本题考查了两条直线相交或平行问题：两条直线的交点坐标，就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解；若两条直线是平行的关系，那么他们的自变量系数相同，即k值相同．例如：若直线y₁=k₁x+b₁与直线y₂=k₂x+b₂平行，那么k₁=k₂．