
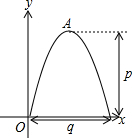
 如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.
如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.分析 (1)根据p、q的值可知其顶点坐标(1,4),设抛物线顶点式,将原点(0,0)代入求解可得;
(2)根据题意知顶点坐标为(1,4+h),设其顶点式y=a(x-1)2+4+h,将原点(0,0)代入后用含h的代数式表示a即可得;
(3)分别求出y=ax2+bx顶点M、y=cx2+dx的顶点N,根据题意知Mx=Nx、My+h=Ny,联立方程求解可得c、d.
解答 解:(1)当p=4,q=2时,抛物线的顶点坐标为(1,4),
设抛物线解析式为y=a(x-1)2+4,
将原点(0,0)代入得:a+4=0,
解得:a=-4,
故抛物线解析式为:y=-4(x-1)2+4;
(2)根据题意知此时抛物线顶点坐标为(1,4+h),
设抛物线解析式为:y=a(x-1)2+4+h,
将原点(0,0)代入,得:a+4+h=0,
解得:a=-(h+4),
故抛物线解析式为:y=-(h+4)(x-1)2+4+h;
(3)∵抛物线y=ax2+bx的顶点坐标为(-$\frac{b}{2a}$,-$\frac{{b}^{2}}{4a}$),
抛物线y=cx2+dx的顶点坐标为(-$\frac{d}{2c}$,-$\frac{{d}^{2}}{4c}$),
∴由题意可知,-$\frac{d}{2c}$=-$\frac{b}{2a}$,即$\frac{d}{c}$=$\frac{b}{a}$ ①,
-$\frac{{d}^{2}}{4c}$=-$\frac{{b}^{2}}{4a}$+h,即$\frac{{d}^{2}}{c}=\frac{{b}^{2}}{a}-4h$ ②,
由①②可得:c=$\frac{a{b}^{2}-4{a}^{2}h}{{b}^{2}}$,d=$\frac{{b}^{2}-4ah}{b}$.
点评 本题主要考查二次函数的应用能力,熟练掌握待定系数法求二次函数解析式及抛物线顶点间的联系是解题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
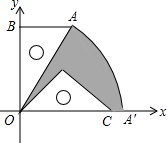 如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)
如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.
如图,⊙O的半径为1,A为⊙O上一点,过点A的直线l交⊙O于点B,将直线l绕点A旋转180°,在旋转过程中,AB的长度由1变为$\sqrt{3}$时,则l在圆内扫过的面积为$\frac{π}{6}$或$\frac{π}{2}$+$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com