
| BC |
| AC |
| BC |
| B1C1 |
| BC |
| B1C1 |
 解:(1)如图所示;(2分)
解:(1)如图所示;(2分)| BC |
| AC |
| DC |
| BC |
| x |
| y |
| y-x |
| x |
-1±
| ||
| 2 |
| x |
| y |
| ||
| 2 |
3-
| ||
| 2 |
| BC |
| AB |
| BC |
| AC |
| ||
| 2 |
| AB |
| AE |
| ||
| 2 |
| BC |
| B1C1 |
| BC |
| AE |
| BC |
| AB |
| AB |
| AE |
| ||
| 2 |
| ||
| 2 |
3-
| ||
| 2 |


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
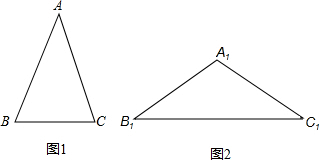
三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.

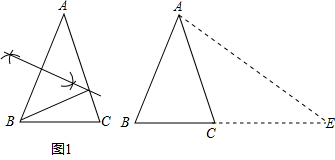
1.在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);
2.△BCD是不是黄金三角形,如果是,请给出证明;如果不是,请说明理由;
3.设![]() ,试求k的值;
,试求k的值;
4.如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,
请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年安徽省马鞍山六中中考模拟数学卷 题型:解答题
三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.
【小题1】在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);
【小题2】△BCD是不是黄金三角形,如果是,请给出证明;如果不是,请说明理由;
【小题3】设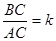 ,试求k的值;
,试求k的值;
【小题4】如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,
请直接写出 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年安徽省中考模拟数学卷 题型:解答题
三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.
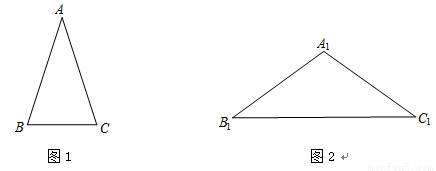
1.在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);
2.△BCD是不是黄金三角形,如果是,请给出证明;如果不是,请说明理由;
3.设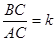 ,试求k的值;
,试求k的值;
4.如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,
请直接写出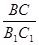 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2013年安徽省中考数学模拟试卷(六)(解析版) 题型:解答题
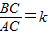 ,试求k的值;
,试求k的值;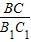 的值.
的值.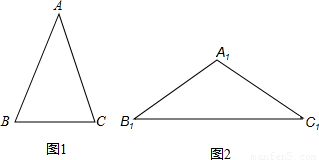
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com