
 x+6交x轴于点A,交y轴于点B.点P,点Q同时从原点出发作匀速运动,点P沿x轴正方向运动,点Q沿OB→BA方向运动,并同时到达点A.点P运动的速度为1厘米/秒.
x+6交x轴于点A,交y轴于点B.点P,点Q同时从原点出发作匀速运动,点P沿x轴正方向运动,点Q沿OB→BA方向运动,并同时到达点A.点P运动的速度为1厘米/秒.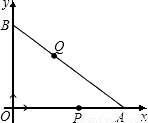
 AQ;又因y=
AQ;又因y= •OP•QE代入相关数据即可求解;
•OP•QE代入相关数据即可求解; ×8=
×8= ×6×8,b=±6,然后分情况讨论:当b=6时,6=-
×6×8,b=±6,然后分情况讨论:当b=6时,6=- x 2+
x 2+ x;所以x=4±
x;所以x=4±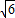 ;当b=-6时,-6=-
;当b=-6时,-6=- x 2+
x 2+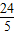 x;所以x=4
x;所以x=4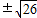 ,所以M(4±
,所以M(4±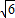 ,6),(4
,6),(4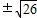 ,-6).
,-6).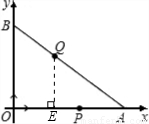
 AQ
AQ •OP•QE=
•OP•QE= •x•
•x• (16-2x)=-
(16-2x)=- x 2+
x 2+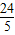 x;
x; x 2+
x 2+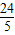 x
x ×8=
×8= ×6×8
×6×8 x 2+
x 2+ x,所以x=4±
x,所以x=4±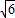 ;
; x 2+
x 2+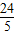 x,所以x=4
x,所以x=4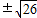 .
.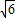 ,6),(4
,6),(4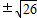 ,-6).
,-6).

科目:初中数学 来源:2009年浙江省宁波市北仑区中考数学二模试卷(解析版) 题型:选择题
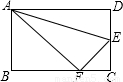




查看答案和解析>>
科目:初中数学 来源:2006年广西河池市中考数学试卷(大纲卷)(解析版) 题型:解答题
 x+6交x轴于点A,交y轴于点B.点P,点Q同时从原点出发作匀速运动,点P沿x轴正方向运动,点Q沿OB→BA方向运动,并同时到达点A.点P运动的速度为1厘米/秒.
x+6交x轴于点A,交y轴于点B.点P,点Q同时从原点出发作匀速运动,点P沿x轴正方向运动,点Q沿OB→BA方向运动,并同时到达点A.点P运动的速度为1厘米/秒.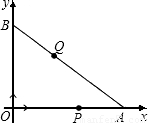
查看答案和解析>>
科目:初中数学 来源:2006年广西河池市中考数学试卷(大纲卷)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2006年广西河池市中考数学试卷(大纲卷)(解析版) 题型:选择题





查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com