
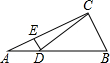
 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,D是AB边上的一个动点(不与点A,B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示与的函数关系的图象大致是( )
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,AB=4,D是AB边上的一个动点(不与点A,B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示与的函数关系的图象大致是( )| A. | 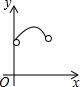 | B. |  | C. | 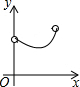 | D. | 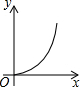 |
科目:初中数学 来源: 题型:选择题
| A. | 4:9或9:25 | B. | 9:25或4:25 | C. | 2:5 | D. | 3:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题:
某知名品牌在甲、乙两地的新店同时开张,乙店经营不久为了差异营销而进行了品牌升级,因此停业了一段时间,随后继续营业,第40天结束时两店销售总收入为2100百元.甲、乙两店自开张后各自的销售收入y(百元)随时间x(天)的变化情况如图所示,请根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 50 | C. | 500 | D. | 250 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com