
如图,∆ABC中,D为AB的中点,E为AC上一点,过D作DF∥BE交AC于O,EF∥AB。

(1)猜想:OD与OF之间的关系是 。
(2)证明你的猜想。
解:(1)OD=OF
(2)∵DF∥BE,EF∥AB
∴四边形DBEF是平行四边形
∴BD=EF
又∵AD=BD
∴AD=EF
又EF∥AB
∴∠DAO=∠FEO
又∠AOD=∠EOF
∴把∆FEO绕点O旋转1800后可与∆DAO重合
∴∆FEO≌∆DAO
∴OF=OD
【解析】(1)0D=OF,
(2)由已知可得四边形BDFE是平行四边形,从而可得BD=EF,由中点的定义可得AD=BD,再根据平行线的性质即可得到∠ADO=∠EFO,∠DAO=∠FEO,从而可利用ASA判定△ADO≌△EFO,根据全等三角形的对应边相等即可得到OD=OF,OA=OE,即得到AE与DF互相平分,或连接AF、DE,然后证明四边形DEFA是平行四边形,再根据平行四边形的对角线互相平分证明.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源:2012年人教版七年级下第七章三角形第一节第二节练习卷(解析版) 题型:选择题
如图,D.E分别为∆ABC的边AC.BC的中点,则下列说法不正确的是( )
A.DE是∆ABC的中线 B.BD是∆ABC的一条中线
C.CE是AB边上的中线 D.BD是边AC上的中线

查看答案和解析>>
科目:初中数学 来源:2010-2011学年浙江省温州市中考模拟数学试卷(解析版) 题型:解答题
如图,Ð1 = Ð2,ÐB = ÐD,AB = DE = 5,BC = 4.

(1)求证:∆ABC∽∆ADE ;
(2)求AD的长。
查看答案和解析>>
科目:初中数学 来源:2013届江苏扬州市江都区八年级下学期期末考试数学试卷(解析版) 题型:解答题
如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为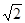 ,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n
,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n

(1)请在图1中找出两对相似而不全等的三角形,并选取其中一对证明它们相似;
(2)根据图1,求m与n的函数关系式,直接写出自变量n的取值范围;
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2). 旋转∆AFG,使得BD=CE,求出D点的坐标,并通过计算验证 ;
;
(4)在旋转过程中,(3)中的等量关系 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com