练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．若两个多边形的边数之比是1：2，内角和度数之和为1440°，求这两个多边形的边数．

    分析 本题根据等量关系“两个多边形的内角之和为1440°”列方程求解，解答时要会根据公式进行正确运算、变形和数据处理．

    解答 解：设多边形较少的边数为n，则
    （n-2）•180°+（2n-2）•180°=1440°，
    解得n=4．
    2n=8．
    故这两个多边形的边数分别为4，8．

    点评 本题考查根据多边形的内角和计算公式求多边形的边数，考查多边形的内角和、方程的思想．关键是记住内角和的公式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．已知4tx-5＞0的解集是x＜-6，则t=-$\frac{5}{24}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知x，y都是实数，且$\sqrt{8-2（x+3）}$与（2y-4）2互为相反数．
    （1）求x，y的值，并写出x，y为边长的等腰三角形的周长；
    （2）求$\frac{1}{x（y+1）}$+$\frac{1}{（x+2）（y+3）}$+$\frac{1}{（x+4）（y+5）}$+…+$\frac{1}{（x+48）（y+49）}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

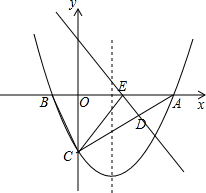    7．已知：如图，对称轴为直线$x=\frac{3}{2}$的抛物线y=ax2+bx+c与x轴交于A、B两点，与y轴交于点C，连接BC、AC，且OB=$\frac{1}{2}$OA=$\frac{1}{3}$OC．
    （1）求抛物线的函数表达式；
    （2）若点P为线段AC上的一点，过P作PM⊥x轴于点M，PQ∥x轴交BC于点Q，再过点Q作QN⊥x轴于点N，求四边形PMNQ为正方形时点P的坐标；
    （3）若动点E从点A出发，沿x轴向点B运动（点E与点A、B不重合），过点E作直线l平行BC，交AC于点D，连接CE．设AE的长为m，求△CDE的面积最大时，点E到直线BC的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

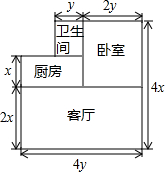    14．（1）一家住房的结构如图所示，这家房子的主人打算把卧室以外的部分都铺上地砖，至少需要多少m2的地砖？如果每1m2地砖的价格是a元钱，则购买所需地砖至少需要多少元？
    （2）已知房屋的高度为h米，现需要在客厅和卧室的墙壁上贴壁纸，那么至少需要多少平方米的壁纸？如果某种壁纸的价格是b元/平方米，那么购买所需要的壁纸至少需要多少元？（计算时不扣除门、窗所占的面积）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．小明的妈妈在菜市场买回3斤萝卜、2斤排骨，准备做萝卜排骨汤．妈妈说：“今天买这两样菜共花了45元，上月买同重量的这两种菜只要36元”；爸爸说：“报纸上说了萝卜的单价上涨50%，排骨单价上涨20%”；小明说：爸爸、妈妈，我想知道今天买的萝卜和排骨的单价分别是多少？
    请你通过列一元一次方程求解这天萝卜、排骨的单价（单位：元/斤）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．如图是小明用火柴搭的1条、2条、3条“金鱼”…，则搭20条“金鱼”需要火柴122根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图．正比例函数y=kx与反比例函数y=$\frac{m}{x}$的图象相交于A（1，a）、C（b，-1）两点，过A作x轴的垂线交x轴于B，连BC．
    （1）a=1；b=-1；△ABC的面积是1．
    （2）求它们的函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．已知直线y=（m-1）x+1-3m，试确定m的值，使得：
    （1）直线经过原点；
    （2）直线与y轴交于（0，2）

    查看答案和解析>>

    同步练习册答案