
【题目】如图,将半径为6的⊙O沿AB折叠,弧AB与AB垂直的半径OC交于点D且CD=2OD,则折痕AB的长为( )
A.![]()
B.![]()
C.6
D.![]()
【答案】B
【解析】延长CO交AB于E点,连接OB,构造直角三角形,然后再根据勾股定理求出AB的长。
延长CO交AB于E点,连接OB,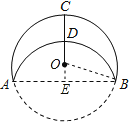
∵CE⊥AB,
∴E为AB的中点,
∵OC=6,CD=2OD,
∴CD=4,OD=2,OB=6,
∴DE=![]() (2OC-CD)=
(2OC-CD)=![]() (6×2-4)=
(6×2-4)=![]() ×8=4,
×8=4,
∴OE=DE-OD=4-2=2,
在Rt△OEB中,
∵OE2+BE2=OB2
∴![]()
∴AB=2BE=![]()
故选B.
【考点精析】本题主要考查了勾股定理的概念和垂径定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,分别以顶点A、B、C、D为圆心,1为半径画弧,四条弧交于点E、F、G、H,则图中阴影部分的外围周长为( )
A.![]()
B.![]()
C.π
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( ) 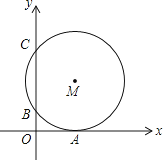
A.10
B.8 ![]()
C.4 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.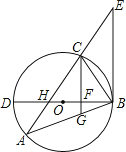
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BGBA=48,FG= ![]() ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名同学在一次用频率去估计概率的实验中,统计了某一结果出现的频率绘出的统计图如图,则符合这一结果的实验可能是( ) 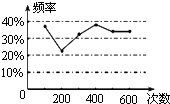
A.掷一枚正六面体的骰子,出现1点的概率
B.抛一枚硬币,出现正面的概率
C.从一个装有2个白球和1个红球的袋子中任取一球,取到红球的概率
D.任意写一个整数,它能被2整除的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com