
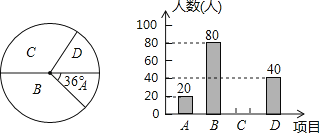
【题目】某学校为了提高学生学科能力,决定开设以下校本课程:A.文学院;B.小小数学家;C.小小外交家;D、未来科学家.为了了解学生最喜欢哪一项校本课程,学校随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次统计共抽查了 名学生;在扇形统计图中,表示C类别的扇形圆心角度数为 .
(2)补全条形统计图;
(3)一班想从表达能力很强的甲、乙、丙、丁四名同学中,任选2名参加小小外交家小组,请用列表或画树状图的方法求恰好同时选中甲、乙两名同学的概率.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是( )
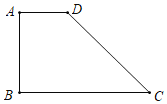
A. 4<OC≤![]() B. 4≤OC≤
B. 4≤OC≤![]() C. 4<OC
C. 4<OC![]() D. 4≤OC
D. 4≤OC![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
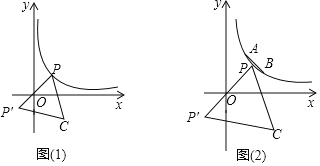
【题目】定义:点P(a,b)关于原点的对称点为P′,以PP′为边作等边△PP′C,则称点C为P的“等边对称点”;
(1)若P(1,3),求点P的“等边对称点”的坐标.
(2)平面内有一点P(1,2),若它其中的一个“等边对称点”C在第四象限时,请求此C点的坐标;
(3)若P点是双曲线y=![]() (x>0)上一动点,当点P的“等边对称点”点C在第四象限时,
(x>0)上一动点,当点P的“等边对称点”点C在第四象限时,
①如图(1),请问点C是否也会在某一函数图象上运动?如果是,请求出此函数的解析式;如果不是,请说明理由.
②如图(2),已知点A (1,2),B (2,1),点G是线段AB上的动点,点F在y轴上,若以A、G、F、C这四个点为顶点的四边形是平行四边形时,求点C的纵坐标yc的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,AD平分∠CAE交⊙O于点D,且AE⊥CD,垂足为点E.
(1)求证:直线CE是⊙O的切线.
(2)若BC=3,CD=3![]() ,求弦AD的长.
,求弦AD的长.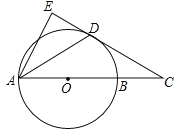
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区2号楼对外销售,已知2号楼某单元共33层,一楼为商铺,只租不售,二楼以上价格如下:第16层售价为6000元/米2,从第16层起每上升一层,每平方米的售价提高30元,反之每下降一层,每平方米的售价降低10元,已知该单元每套的面积均为100米2
(1)请在下表中,补充完整售价y(元/米2)与楼层x(x取正整数)之间的函数关系式.
楼层x(层) | 1楼 | 2≤x≤15 | 16楼 | 17≤x≤33 |
售价y(元/米2) | 不售 |
| 6000 |
|
(2)某客户想购买该单元第26层的一套楼房,若他一次性付清购房款,可以参加如图优惠活动.请你帮助他分析哪种优惠方案更合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4与x轴交于点A(﹣1,0)、B(3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)如图1,D为抛物线对称轴上一动点,求D运动到什么位置时△DAC的周长最小;
(3)如图2,点E在第一象限抛物线上,AE与BC交于点F,若AF:FE=2:1,求E点坐标;
(4)点M、N同时从B点出发,分别沿BA、BC方向运动,它们的运动速度都是1个单位/秒,当点M运动到点A时,点N停止运动,则当点N停止运动后,在x轴上是否存在点P,使得△PBN是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
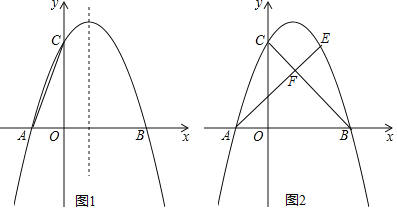
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一科技小组进行了机器人行走性能试验.在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,经过7min同时到达C点,乙机器人始终以60m/min的速度行走,如图是甲、乙两机器人之间的距离y(m)与他们的行走时间x(min)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 .m,甲机器人前2min的速度为 .m/min;
(2)若前3min甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)直接写出两机器人出发多长时间相距28m.
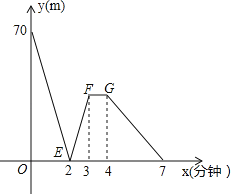
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+4x+c过点A(6,0)、B(3,![]() ),与y轴交于点C.联结AB并延长,交y轴于点D.
),与y轴交于点C.联结AB并延长,交y轴于点D.
(1)求该抛物线的表达式;
(2)求△ADC的面积;
(3)点P在线段AC上,如果△OAP和△DCA相似,求点P的坐标.
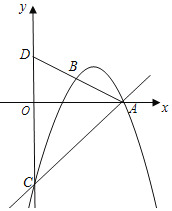
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如果函数![]() 满足:对于自变量
满足:对于自变量![]() 的取值范围内的任意
的取值范围内的任意![]() ,
,![]() ,
,
(1)若![]() ,都有
,都有![]() ,则称
,则称![]() 是增函数;
是增函数;
(2)若![]() ,都有
,都有![]() ,则称
,则称![]() 是减函数.
是减函数.
例题:证明函数![]() 是减函数.
是减函数.
证明:设![]() ,
,
![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .即
.即![]() .
.
∴![]() .
.
∴函数![]() 是减函数.
是减函数.
根据以上材料,解答下面的问题:
已知函数![]() ,
,
![]() ,
,![]()
(1)计算:![]() ,
,![]() ;
;
(2)猜想:函数![]() 是 函数(填“增”或“减”);
是 函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com