
【题目】如图,AB是⊙O的直径,弦CD⊥AB ,垂足为H,连接AC,过![]() 上一点E作 EG∥AC 交CD的延长线于点G,连接AE交CD于点F,且EG=FG .
上一点E作 EG∥AC 交CD的延长线于点G,连接AE交CD于点F,且EG=FG .
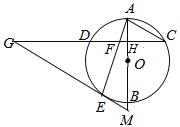
(1)求证:EG是 ⊙O 的切线;
(2)延长AB交GE的延长线于点M ,若tanG=![]() ,AH=2,求 EM 的值.
,AH=2,求 EM 的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】分析:(1)欲证明EG是⊙O的切线只要证明EG⊥OE即可;
(2)连接OC.设⊙O的半径为r.在Rt△OCH中,利用勾股定理求出r,证明△AHC∽△MEO,可得![]() ,由此即可解决问题.
,由此即可解决问题.
详解:(1)如图,连接OE,
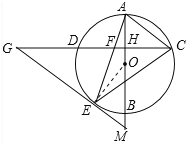
∵GF=GE,
∴∠GFE=∠GEF=∠AFH,
∵OA=OE,
∴∠OAE=∠OEA,
∵AB⊥CD,
∴∠AFH+∠FAH=90°,
∴∠GEF+∠AEO=90°,
∴∠GEO=90°
∴GE⊥OE,
∴EG是⊙O的切线;
(2)如图,连接OC.
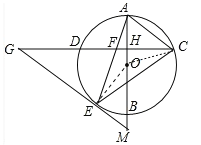
设⊙O的半径为r,
在Rt△AHC中,tan∠ACH=tan∠G=![]() ,
,
∵AH=2,
∴HC=4,
在Rt△HOC中,
∵OC=r,OH=r-2,HC=4,
∴![]() ,
,
∴r=5,
∵GM∥AC,
∴∠CAH=∠M,
∵∠OEM=∠AHC,
∴△AHC∽△MEO
∴![]() ,
,
∴![]() ,
,
∴EM=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,CD平分∠ACB交⊙O于点D.
(1)AD与BD相等吗?为什么?
(2)若AB=10,AC=6,求CD的长;
(3)若P为⊙O上异于A、B、C、D的点,试探究PA、PD、PB之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
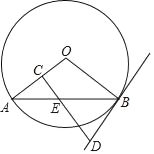
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线L上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4 , 则S1+2S2+2S3+S4=()
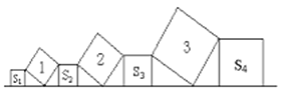
A. 5 B. 4 C. 6 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场准备购进A、B两种商品进行销售,若A种商品的进价比B种商品的进价每件少 5元,且用 90元购进A种商品的数量比用100元购进B种商品的数量多1件.
(1)求A、B两种商品的进价每件分别是多少元?
(2)若该商场购进A种商品的数量是B种商品数量的3倍少4 件,两种商品的总件数不超过96件;A种商品的销售价格为每件30元,B种商品的销售价格为每件38元,两种商品全部售出后,可使总利润超过1200元.该商场购进A、B两种商品有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市有着丰富的土地资源,适宜种植玉米,某企业已收购玉米52.5吨,根据市场信息,将玉米直接销售,每吨可获利100元;如果对玉米进行粗加工,每天可加工8吨,每吨可获利1000元;如果对玉米进行精加工,每天可加工0.5吨,每吨可获利5000元.由于受条件限制,在同一天中只能采取一种加工方式,并且必须在30天内将这批玉米全部销售,为此,研究了两种方案.
(1)方案一:将玉米全部粗加工后销售,则可获利 元;
(2)方案二:30天时间都进行精加工,未来得及加工的玉米,在市场上直接销售,则可获利 元;
(3)问是否存在第三种方案,将部分玉米精加工,其余玉米粗加工,并恰好在30天内完成?若存在,请求销售后所获利润:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
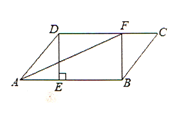
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求tan∠BAF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),CN⊥DM,CN与AB交于点N,连接OM、ON、MN.下列四个结论:①△CNB≌△DMC;②△CON≌△DOM;③AN2+CM2=MN2;④若AB=2,则S△OMN的最小值是![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
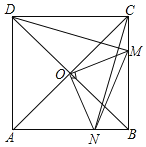
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x+b与双曲线![]() 相交于A(1,2),B(m,-1)两点.
相交于A(1,2),B(m,-1)两点.

(1)求直线和双曲线的表达式;
(2)求直线AB与x轴的交点C的坐标及ΔAOB的面积;
(3)观察图像,请直接写出使不等式k1x+b>![]() 成立的x的取值范围.
成立的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com