
【题目】成都市中心城区“小游园,微绿地”规划已经实施,武侯区某街道有一块矩形空地进入规划试点.如图,已知该矩形空地长为![]() ,宽为
,宽为![]() ,按照规划将预留总面积为
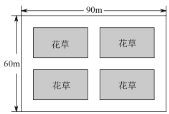
,按照规划将预留总面积为![]() 的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
的四个小矩形区域(阴影部分)种植花草,并在花草周围修建三条横向通道和三条纵向通道,各通道的宽度相等.
(1)求各通道的宽度;
(2)现有一工程队承接了对这![]() 的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了
的区域(阴影部分)进行种植花草的绿化任务,该工程队先按照原计划进行施工,在完成了![]() 的绿化任务后,将工作效率提高
的绿化任务后,将工作效率提高![]() ,结果提前
,结果提前![]() 天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
天完成任务,求该工程队原计划每天完成多少平方米的绿化任务?
【答案】(1)各通道的宽度为![]() 米;(2)原计划每天完成
米;(2)原计划每天完成![]() 平方米的绿化任务.
平方米的绿化任务.
【解析】
(1)设各通道的宽度为x米,将四个小矩形合并成一个大矩形,则大矩形的长为(90-3x)cm,宽为(60-3x)cm,再根据矩形面积公式列方程求解即可;
(2)设该工程队原计划每天完成ym2的绿化任务,则按原计划完成任务需要![]() 天,完成
天,完成![]() 的绿化任务需要
的绿化任务需要![]() 天,提高工作效率后完成剩余工作量所需要的时间为
天,提高工作效率后完成剩余工作量所需要的时间为![]() 天,再按照题干所给时间关系列出方程并求解即可.
天,再按照题干所给时间关系列出方程并求解即可.
解:(1)设各通道的宽度为x米,将四个小矩形合并成一个大矩形,则可得方程,
(90-3x)(60-3x)=4536,解得x=2或48(不合题意,舍去),
故各通道的宽度为![]() 米;
米;
(2)设该工程队原计划每天完成ym2的绿化任务,则由题干条件得,
![]() ,解得y=400m2/天,
,解得y=400m2/天,
经检验,y=400m2/天是原方程的解,并符合题意,
故原计划每天完成![]() 平方米的绿化任务.
平方米的绿化任务.


科目:初中数学 来源: 题型:
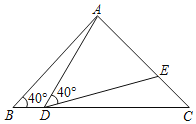
【题目】如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE与AC交于E.
(1)当∠BDA=115°时,∠BAD=_____°,∠DEC=_____°;当点D从B向C运动时,∠BDA逐渐变______(填”大”或”小”);
(2)当DC=AB=2时,△ABD与△DCE是否全等?请说明理由:
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒?四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋有![]() 个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了
个黑球和若干个白球,在不允许将球倒出来的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,再放回口袋中,…,不断重复上述过程,小明共摸了![]() 次,其中
次,其中![]() 次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________.
次摸到黑球.根据上述数据,小明正估计口袋中的白球的个数是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
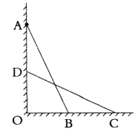
【题目】王涵想知道一堵墙上点![]() 的高度,即
的高度,即![]() 的长度
的长度![]() ,但点
,但点![]() 的位置较高,没有梯子之类的工具,于是设计了下面的方案,请你先补全方案,再说明理由.
的位置较高,没有梯子之类的工具,于是设计了下面的方案,请你先补全方案,再说明理由.
(1)补全方案.
第一步:如图,找一根长度大于![]() 的直杆,使直杆靠在墙上,且顶端与点
的直杆,使直杆靠在墙上,且顶端与点![]() 重合,记下直杆与地面的夹角
重合,记下直杆与地面的夹角![]() ;
;
第二步:使直杆顶端竖直缓慢下滑,直到![]() __________
__________![]() __________,标记此时直杆的底端点
__________,标记此时直杆的底端点![]() ;
;
第三步:测量__________的长度,即为点![]() 的高度;
的高度;
(2)说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(解决问题)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
,![]() 为边,分别作正三角形
为边,分别作正三角形![]() 和正三角形
和正三角形![]() ,连接
,连接![]() ,
,![]() .
.
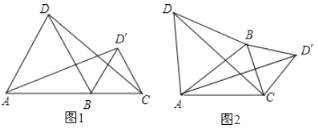
(1)如图1,当点![]() ,
,![]() ,
,![]() 在同一直线上时,线段
在同一直线上时,线段![]() 与
与![]() 的大小关系是__________;
的大小关系是__________;
(2)如图2,当![]() ,
,![]() ,
,![]() 为三角形的顶点时(点
为三角形的顶点时(点![]() ,
,![]() ,
,![]() 不在同一条直线上),判断线段
不在同一条直线上),判断线段![]() 与
与![]() 的大小关系是否发生改变,并说明理由;
的大小关系是否发生改变,并说明理由;
(类比猜想)
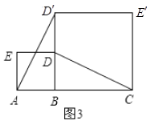
(3)已知![]() ,
,![]() ,
,![]() 是同一平面上的三个点,以线段
是同一平面上的三个点,以线段![]() ,
,![]() 为边,分别作正方形,连接
为边,分别作正方形,连接![]() ,
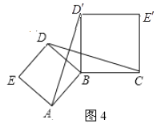
,![]() ,如图3和图4所示.判断线段
,如图3和图4所示.判断线段![]() 与
与![]() 的大小关系,并在图4(点
的大小关系,并在图4(点![]() ,
,![]() ,
,![]() 不在同一条直线上)中证明你的判断;
不在同一条直线上)中证明你的判断;
(推广应用)(4)上面的这些结论能否推广到任意正多边形(不必证明)?
(5)如图5,![]() 与
与![]() 的大小关系是__________,并写出它们分别在哪两个全等三角形中;
的大小关系是__________,并写出它们分别在哪两个全等三角形中;
(6)请在图6中连接图中两个顶点,构造处一组全等三角形,并写出这两个全等的三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
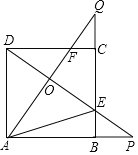
【题目】如图,正方形ABCD的边长是![]() ,连接
,连接![]() 交于点O,并分别与边
交于点O,并分别与边![]() 交于点
交于点![]() ,连接AE,下列结论:
,连接AE,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 当
当![]() 时,
时, ![]() ,其中正确结论的个数是
,其中正确结论的个数是![]()
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:
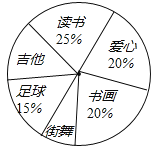
(1)该班的学生共有 名;
(2)若该班参加“吉他社”与“街舞社”的人数相同,请你计算,“吉他社”对应扇形的圆心角的度数;
(3)901班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com