
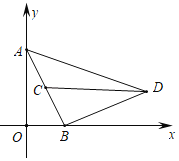
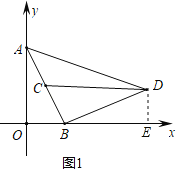
ЎѕМвДїЎїФЪЖЅГжЦ±ЅЗЧш±кПµЦРЈ¬ПЯ¶ОABµДБЅёц¶ЛµгAЈЁ0Ј¬2Ј©Ј¬BЈЁ1Ј¬0Ј©Ј¬µгCОЄПЯ¶ОABµДЦРµгЈ®Ѕ«ПЯ¶ОBAИЖµгB°ґЛіК±Хл·ЅПтРэЧЄ90ЎгµГµЅПЯ¶ОBDЈ¬Б¬ЅбCDЈ¬ADЈ®µгPКЗЦ±ПЯBDЙПµДТ»ёц¶ЇµгЈ®
ЈЁ1Ј©ЗуµгDµДЧш±кєНЦ±ПЯBDµДЅвОцКЅЈ»
ЈЁ2Ј©µ±ЎПPCDЈЅЎПADCК±Ј¬ЗуµгPµДЧш±кЈ»
ЈЁ3Ј©ИфµгQКЗѕ№эµгBЈ¬µгDµДЕЧОпПЯyЈЅax2+bx+2ЙПµДТ»ёц¶ЇµгЈ¬ЗлДгМЅЛчЈєКЗ·сґжФЪХвСщµДµгQЈ¬К№µГТФµгPЎўµгQЎўµгDОЄ¶ҐµгµДИэЅЗРОУлЎчACDПаЛЖЈ®ИфґжФЪЈ¬ЗлЗуіцµгPµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©µгPµДЧш±кОЄЈЁ2Ј¬
Ј»ЈЁ2Ј©µгPµДЧш±кОЄЈЁ2Ј¬![]() Ј©»тЈЁ8Ј¬
Ј©»тЈЁ8Ј¬![]() Ј©Ј»ЈЁ3Ј©јыЅвОц.
Ј©Ј»ЈЁ3Ј©јыЅвОц.
ЎѕЅвОцЎї
ЈЁ1Ј©ЧчDEЎНxЦбЈ¬№№ФмИ«µИИэЅЗРОЗуµгDµДЧш±кЈ¬ґэ¶ЁПµКэ·ЁЗуBDµДЅвОцКЅЈ»
ЈЁ2Ј©ТЄМШ±рЧўТвЎПPCDЈЅЎПADCУРБЅЦЦЗйїцЈєЎПPCDФЪЦ±ПЯCDµДПВ·Ѕ»тЙП·ЅЈ¬·АЦ№В©ЅвЈ»
ЈЁ3Ј©ёщѕЭЎПPDQ·Ц±рУлЎПACDЈ¬ЎПADCЈ¬ЎПCADПаµИЅшРРМЦВЫЈ¬ГїЦЦЗйРО¶ј»№ТЄФЩ·ЦБЅЦЦЗйїцЅшРР·ЦОцЈ¬»№ТЄЧўТвµгФЪµгDµДЧуІаєНУТІаБЅЦЦІ»Н¬ЗйїцЈ¬ТФ·АВ©ЅвЈ®
ЅвЈєЈЁ1Ј©ИзНј1Ј¬№эDЧчDEЎНxЦбУЪEЈ¬УЙРэЧЄµГЈєBAЈЅBDЈ¬ЎПABDЈЅ90ЎгЈ¬
ЎЯDEЎНxЦбЈ¬
ЎаЎПBEDЈЅЎПAOBЈЅ90Ўг
ЎаЎПBAO+ЎПABOЈЅ90ЎгЈ¬ЎПDBE+ЎПABOЈЅ90ЎгЈ¬
ЎаЎПBAOЈЅЎПDBE
ЎаЎчBAOЎХЎчDBEЈЁAASЈ©
ЎаBEЈЅOAЈЅ2Ј¬DEЈЅOBЈЅ1Ј¬
ЎаOEЈЅOB+BEЈЅ1+2ЈЅ3
ЎаDЈЁ3Ј¬1Ј©Ј»
ЙиЦ±ПЯBDµДЅвОцКЅОЄyЈЅmx+nЈ¬Ѕ«BЈЁ1Ј¬0Ј©Ј¬DЈЁ3Ј¬1Ј©·Ц±рґъИлµГ![]() Ј¬ЅвµГ
Ј¬ЅвµГ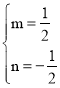 Ј¬
Ј¬
ЎаЦ±ПЯBDµДЅвОцКЅОЄ![]() Ј®
Ј®
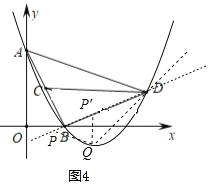
ЈЁ2Ј©ИзНј2Ј¬ЎЯЎПPCDЈЅЎПADC
ЎаCPЎОAD
Ўа![]() Ј¬
Ј¬
ЎЯBCЈЅCA
ЎаBPЈЅPD
ЎаPЈЁ2Ј¬![]() Ј©Ј¬
Ј©Ј¬
ЧчµгP№ШУЪЦ±ПЯCDµД¶ФіЖµгPЎдЈЁ2Ј¬![]() Ј©Ј¬Б¬ЅУCPЎдЈ¬ФтЎПPЎдCDЈЅЎПPCDЈЅЎПADC
Ј©Ј¬Б¬ЅУCPЎдЈ¬ФтЎПPЎдCDЈЅЎПPCDЈЅЎПADC
ЙиЦ±ПЯCPЎдµДЅвОцКЅОЄyЈЅm1x+n1Ј¬Ѕ«CЈЁ![]() Ј¬1Ј©Ј¬PЎдЈЁ2Ј¬
Ј¬1Ј©Ј¬PЎдЈЁ2Ј¬![]() Ј©ґъИлµГ
Ј©ґъИлµГ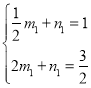 Ј¬ЅвµГ
Ј¬ЅвµГ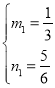 Ј¬
Ј¬
ЎаЦ±ПЯCPЎдµДЅвОцКЅОЄ![]() Ј¬
Ј¬
БЄБў·ЅіМЧй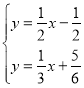 Ј¬ЅвµГ
Ј¬ЅвµГ![]() Ј¬ЎаPЈЁ8Ј¬
Ј¬ЎаPЈЁ8Ј¬![]() Ј©Ј¬
Ј©Ј¬
ЧЫЙПЛщКцЈєµгPµДЧш±кОЄЈЁ2Ј¬![]() Ј©»тЈЁ8Ј¬
Ј©»тЈЁ8Ј¬![]() Ј©Ј®
Ј©Ј®
ЈЁ3Ј©Ѕ«BЈЁ1Ј¬0Ј©Ј¬DЈЁ3Ј¬1Ј©·Ц±рґъИлyЈЅax2+bx+2µГ![]() Ј¬
Ј¬
ЅвµГ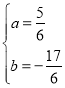 Ј¬
Ј¬
ЎаЕЧОпПЯЅвОцКЅОЄ![]() Ј¬
Ј¬
ЎчPDQУлЎчACDПаЛЖ·ЦИэЦЦЗйїцЈє
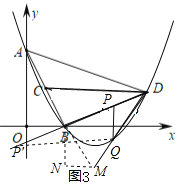
ўЩИзНј3Ј¬ЎПPDQЈЅЎПDACЈЅ45ЎгЈ¬СУі¤ABЦБMЈ¬К№BMЈЅBDЈ¬Б¬ЅУDMЅ»ЕЧОпПЯУЪQЈ¬
ЧчBNЎОyЦбЈ¬MNЎОxЦбЅ»BNУЪNЈ¬
ЎаBMЈЅBDЈЅ![]() Ј¬ЎПMBNЈЅЎПBAOЈ¬ЎПBNMЈЅ90Ўг
Ј¬ЎПMBNЈЅЎПBAOЈ¬ЎПBNMЈЅ90Ўг
Ўа![]() ЈЅtanЎПMBNЈЅtanЎПBAOЈЅ
ЈЅtanЎПMBNЈЅtanЎПBAOЈЅ![]() Ј¬
Ј¬
ЎаMNЈЅ1Ј¬BNЈЅ2Ј¬
ЎаMЈЁ2Ј¬©Ѓ2Ј©Ј»
ЙиЦ±ПЯDMЅвОцКЅОЄyЈЅm2x+n2Ј¬Ѕ«DЈЁ3Ј¬1Ј©ЎўMЈЁ©Ѓ2Ј¬©Ѓ2Ј©ґъИлЈ¬
µГ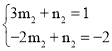 Ј¬
Ј¬
ЅвµГ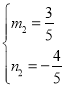
ЎаЦ±ПЯDMЅвОцКЅОЄ![]()
БЄБў·ЅіМЧй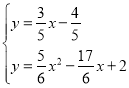 Ј¬
Ј¬
ЅвµГ![]() ЈЁЙбИҐЈ©Ј¬
ЈЁЙбИҐЈ©Ј¬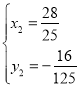
Q![]() Ј»
Ј»
ИфЎПDPQЈЅЎПACDЈ¬ФтїЙЦ¤µГPQЎОyЦбЈ¬
ЎаP1![]() Ј¬
Ј¬
ИфЎПDPQЈЅЎПADCЈ¬їЙЗуµГ
P2![]() Ј¬
Ј¬
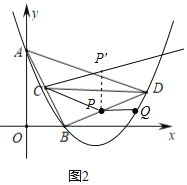
ўЪЎПPDQЈЅЎПADCК±Ј¬
ИзНј4Ј¬µгQО»УЪЦ±ПЯBDПВ·ЅК±Ј¬
ЎПPDQ+ЎПCDBЈЅЎПADC+ЎПCDBЈ¬јґЎПCDQЈЅЎПADBЈЅ45ЎгЈ¬
ЎЯCDЎОxЦбЈ¬ЎаЦ±ПЯDQУлxЦбјРЅЗОЄ45ЎгЈ¬ЙиDQЅвОцКЅОЄyЈЅx+kЈ¬Ѕ«DЈЁ3Ј¬1Ј©ґъИлµГ3+kЈЅ1Ј¬kЈЅ©Ѓ2
ЎаyЈЅx©Ѓ2
БЄБў·ЅіМЧй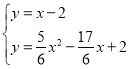 Ј¬
Ј¬
ЅвµГ![]() ЈЁЙбИҐЈ©Ј¬
ЈЁЙбИҐЈ©Ј¬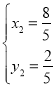 Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
ТЧЗуЦ±ПЯADЅвОцКЅОЄ![]() Ј¬
Ј¬
ЎаЦ±ПЯPQЅвОцКЅОЄ![]()
БЄБў·ЅіМЧй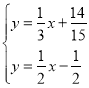 Ј¬ЅвµГ
Ј¬ЅвµГ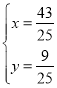 Ј¬
Ј¬
ЎаP3![]() Ј¬
Ј¬
ИфЎПDPQЈЅЎПACDЈ¬ФтPQЎОyЦбЈ¬![]() Ј»
Ј»
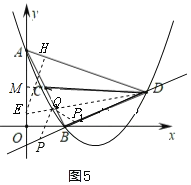
ИзНј5Ј¬µгQО»УЪЦ±ПЯBDЙП·ЅК±Ј¬
ФЪyЦбЙПИЎµгEЈЁ0Ј¬![]() Ј©Ј¬СУі¤DCЅ»yЦбУЪµгMЈ¬Б¬ЅУDEЅ»ЕЧОпПЯУЪQЈ¬№эµгEЧчEHЎНADУЪHЈ¬
Ј©Ј¬СУі¤DCЅ»yЦбУЪµгMЈ¬Б¬ЅУDEЅ»ЕЧОпПЯУЪQЈ¬№эµгEЧчEHЎНADУЪHЈ¬
ЧчЎПDQP1ЈЅ45Ўг»тЎПDQPЈЅЎПACDЈ¬µгPЈ¬P1ФЪЦ±ПЯBDЙПЈ¬
ФЪRtЎчAEHЦРЈ¬tanЎПADMЦРЈ¬tanЎПDAMЈЅ![]() ЈЅ3Ј¬AMЈЅ1Ј¬DMЈЅ3Ј¬AMЈЅ
ЈЅ3Ј¬AMЈЅ1Ј¬DMЈЅ3Ј¬AMЈЅ![]() Ј»
Ј»
ФЪRtЎчAEHЦРЈ¬tanЎПEADЈЅ![]() ЈЅ3Ј¬AEЈЅAO©ЃOEЈЅ2©Ѓ
ЈЅ3Ј¬AEЈЅAO©ЃOEЈЅ2©Ѓ![]() Ј¬
Ј¬
ЙиAHЈЅxЈ¬ФтEHЈЅ3xЈ¬
УЙ№ґ№Й¶ЁАнµГ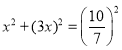 Ј¬ЅвµГxЈЅ
Ј¬ЅвµГxЈЅ![]() Ј¬
Ј¬
ЎаEHЈЅ![]() Ј¬DHЈЅ
Ј¬DHЈЅ![]()
ЎаtanЎПEDAЈЅ![]() ЈЅtanЎПBAC
ЈЅtanЎПBAC
ЎаЎПEDAЈЅЎПBAC
ЎаЎПBDQЈЅЎПADC
ТЧЗуµГЦ±ПЯDEЅвОцКЅОЄyЈЅ![]() Ј¬їЙБЄБў·ЅіМЧйЅвµГQ
Ј¬їЙБЄБў·ЅіМЧйЅвµГQ![]() ,
,
ИфЎПDQPЈЅЎПDACЈЅ45ЎгЈ¬ТЧЗуµГDQЈЅ![]() Ј¬
Ј¬
УЙЎчADCЎЧЎчQDPµГ![]() Ј¬
Ј¬
ЎаDPЎБDAЈЅDCЎБDQЈ¬јґ![]() Ј¬
Ј¬
ЎаDPЈЅ![]()
ЎаP5![]() Ј®
Ј®
ИфЎПDPQЈЅЎПDACЈЅ45ЎгЈ¬
УЙЎчDPQЎЧЎчDACµГ![]()
ЎаDPЎБDCЈЅDAЎБDQЈ¬јґDPЎБ![]()
ЎаDPЈЅ![]()
ЎаP6![]()
ўЫИзНј6Ј¬ЎПPDQЈЅЎПACDЈ¬
µ±µгPФЪЙдПЯDBЙПК±Ј¬
ЎЯЎПACDЈЅЎПCDB+ЎПCBDЈЅЎПCDB+90Ўг
ЎаDQЎНCDК±Ј¬ЎПBDQЈЅЎПACDЈ¬ПФИ»Ј¬ґЛК±µгQІ»ґжФЪЈ®
µ±µгPФЪDB·ґПтСУі¤ПЯЙПК±Ј¬
ТЧЗуµГЦ±ПЯDQЅвОцКЅОЄyЈЅ![]() ,
,
БЄБў·ЅіМЧйїЙЗуµГQ![]() Ј¬
Ј¬
ЎаDQЈЅ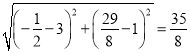
ИфЎПPQDЈЅЎПADCЈ¬ФтЎчDPQЎЧЎчCAD
Ўа![]() Ј¬јґDPЎБCDЈЅCAЎБDQЈ¬DPЎБ
Ј¬јґDPЎБCDЈЅCAЎБDQЈ¬DPЎБ![]()
ЎаDPЈЅ![]()
ЎаP7![]() Ј¬
Ј¬
ИфЎПPQDЈЅЎПDACЈ¬ФтЎчDPQЎЧЎчCDA
Ўа![]() Ј¬јґDPЎБCAЈЅCDЎБDQЈ¬DPЎБ
Ј¬јґDPЎБCAЈЅCDЎБDQЈ¬DPЎБ![]()
ЎаDPЈЅ![]()
ЎаP8![]()
ЧЫЙПЛщКцЈє·ыєПТЄЗуµДµгPµДЧш±кОЄP1![]() ,P2
,P2![]() Ј¬P3
Ј¬P3![]() Ј¬
Ј¬![]() Ј» P5
Ј» P5![]() Ј¬P6
Ј¬P6![]() Ј¬P7
Ј¬P7![]() Ј¬P8
Ј¬P8![]() Ј®
Ј®



 ФД¶БїміµПµБРґр°ё
ФД¶БїміµПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ABКЗ°лФІOµДЦ±ѕ¶Ј¬µгPКЗ°лФІЙПІ»УлµгAЈ¬BЦШєПµД¶ЇµгЈ¬PCЎОABЈ¬µгMКЗOPЦРµгЈ®
ЈЁ1Ј©ЗуЦ¤ЈєЛД±ЯРОOBCPКЗЖЅРРЛД±ЯРОЈ»
ЈЁ2Ј©МоїХЈє
ўЩµ±ЎПBOPЈЅЎЎ ЎЎК±Ј¬ЛД±ЯРОAOCPКЗБвРОЈ»
ўЪБ¬ЅУBPЈ¬µ±ЎПABPЈЅЎЎ ЎЎК±Ј¬PCКЗЎСOµДЗРПЯЈ®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїємРЗ№«ЛѕЙъІъµДДіЦЦК±БоЙМЖ·ГїјюіЙ±ѕОЄ20ФЄЈ¬ѕ№эКРіЎµчСР·ўПЦЈ¬ХвЦЦЙМЖ·ФЪОґАґ40МмДЪµД ИХПъКЫБї(јю)УлК±јд(Мм)µД№ШПµИзПВ±нЈє
К±јд(Мм) | 1 | 3 | 6 | 10 | 36 | Ў |
ИХПъКЫБї(јю) | 94 | 90 | 84 | 76 | 24 | Ў |
ОґАґ40МмДЪЈ¬З°20МмГїМмµДјЫёсy1(ФЄ/јю)УлtК±јд(Мм)µДєЇКэ№ШПµКЅОЄЈєy1=![]() t+25(1ЎЬtЎЬ20ЗТtОЄХыКэ)Ј»єу20МмГїМмµДјЫёсy2(Ф/јю)УлtК±јд(Мм)µДєЇКэ№ШПµКЅОЄЈєy2=ЎЄ
t+25(1ЎЬtЎЬ20ЗТtОЄХыКэ)Ј»єу20МмГїМмµДјЫёсy2(Ф/јю)УлtК±јд(Мм)µДєЇКэ№ШПµКЅОЄЈєy2=ЎЄ![]() t+40(21ЎЬtЎЬ40ЗТtОЄХыКэ).ПВГжОТГЗАґСРѕї ХвЦЦЙМЖ·µДУР№ШОКМв.
t+40(21ЎЬtЎЬ40ЗТtОЄХыКэ).ПВГжОТГЗАґСРѕї ХвЦЦЙМЖ·µДУР№ШОКМв.
(1)ИПХж·ЦОцЙП±нЦРµДКэБї№ШПµЈ¬АыУГС§№эµДТ»ґОєЇКэЎў¶юґОєЇКэ Ўў·ґ±ИАэєЇКэµДЦЄК¶И·¶ЁТ»ёцВъЧгХвР©КэѕЭЦ®јдµДєЇКэ№ШПµКЅЈ»
(2)ЗлФ¤ІвОґАґ40МмЦРДЗТ»МмµДПъКЫАыИуЧоґуЈ¬ЧоґуИХПъКЫАыИуКЗ¶аЙЩЈї
(3)ФЪКµјКПъКЫµДЗ°20МмЦРёГ№«Лѕѕц¶ЁГїПъКЫТ»јюЙМЖ·ѕНѕиФщaФЄАыИу(aЈј4)ёшПЈНы№¤іМЈ¬№«ЛѕНЁ№эПъКЫјЗВј·ўПЦЈ¬З°20МмЦРЈ¬ГїМмїЫіэѕиФщєуµДИХПъКЫАыИуЛжК±јдtµДФцґу¶шФцґуЈ¬ЗуaµДИЎЦµ·¶О§.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪТ»Мх±КЦ±µД¶«ОчПтєЈ°¶ПЯlЙПУРТ»і¤ОЄ1.5kmµДВлН·MNєНµЖЛюCЈ¬µЖЛюCѕаВлН·µД¶«¶ЛNУР20km.Т»ВЦґ¬ТФ36km/hµДЛЩ¶ИєЅРРЈ¬ЙПОз10Јє00ФЪAґ¦ІвµГµЖЛюCО»УЪВЦґ¬µД±±Ж«Оч30Ўг·ЅПтЈ¬ЙПОз10Јє40ФЪBґ¦ІвµГµЖЛюCО»УЪВЦґ¬µД±±Ж«¶«60Ўг·ЅПтЈ¬ЗТУлµЖЛюCПаѕа12km.
(1)ИфВЦґ¬ХХґЛЛЩ¶ИУлєЅПтєЅПтЈ¬єОК±µЅґпєЈ°¶ПЯЈї
(2)ИфВЦґ¬І»ёД±дєЅПтЈ¬ёГВЦґ¬ДЬ·сНЈїїФЪВлН·ЈїЗлЛµГчАнУЙ(ІОїјКэѕЭЈє ![]() ЎЦ1.4Ј¬
ЎЦ1.4Ј¬ ![]() ЎЦ1.7)Ј®
ЎЦ1.7)Ј®

Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЎчABCЦРЈ¬ABЈЅ![]() Ј¬BCЈЅ6Ј¬ЎПBЈЅ45ЎгЈ¬DОЄBC±ЯЙПТ»µгЅ«ЎчABCСШЧЕ№эDµгµДЦ±ПЯХЫµюЈ¬К№µГµгCВдФЪAB±ЯЙПЈ¬јЗCDЈЅmЈ¬ФтACЈЅ_____Ј¬mµДИЎЦµ·¶О§КЗ_____
Ј¬BCЈЅ6Ј¬ЎПBЈЅ45ЎгЈ¬DОЄBC±ЯЙПТ»µгЅ«ЎчABCСШЧЕ№эDµгµДЦ±ПЯХЫµюЈ¬К№µГµгCВдФЪAB±ЯЙПЈ¬јЗCDЈЅmЈ¬ФтACЈЅ_____Ј¬mµДИЎЦµ·¶О§КЗ_____
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїОЄБЛХЖОХ°ЛДкј¶КэС§їјКФѕнµДГьМвЦКБїУлДС¶ИПµКэЈ¬ГьМвЧйЅМК¦ё°НвµШСЎИЎТ»ёцЛ®ЖЅПаµ±µД°ЛДкј¶°ај¶ЅшРРФ¤ІвЈ¬Ѕ«їјКФіЙјЁ·ЦІјЗйїцЅшРРґ¦Ан·ЦОцЈ¬ЦЖіЙЖµКэ·ЦІј±нИзПВ(іЙјЁµГ·ЦѕщОЄХыКэ)Јє
Чй±р | іЙјЁ·ЦЧй | ЖµКэЖµВК | ЖµКэ |
1 |
| 2 | 0.05 |
2 |
| 4 | 0.10 |
3 |
|
| 0.2 |
4 |
| 10 | 0.25 |
5 |
|
|
|
6 |
| 6 | 0.15 |
єПјЖ | 40 | 1.00 |
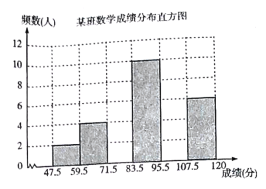
ёщѕЭ±нЦРМṩµДРЕПўЅвґрПВБРОКМвЈє
ЈЁ1Ј©ЖµКэ·ЦІј±нЦРµД![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј»
Ј»
ЈЁ2Ј©ТСЦЄИ«Зш°ЛДкј¶№ІУР200ёц°а(ЖЅѕщГї°а40ИЛ)Ј¬УГХв·ЭКФѕнјмІвЈ¬108·Цј°ТФЙПОЄУЕРгЈ¬Ф¤јЖУЕРгµДИЛКэФјОЄ Ј¬72·Цј°ТФЙПОЄј°ёсЈ¬Ф¤јЖј°ёсµДИЛКэФјОЄ Ј¬ј°ёсµД°Щ·Ц±ИФјОЄ Ј»
ЈЁ3Ј©І№ідНкХыЖµКэ·ЦІјЦ±·ЅНј.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЦР»ЄОД»ЇФґФ¶Бчі¤Ј¬ОДС§·ЅГжЈ¬Ў¶ОчУОјЗЎ·ЎўЎ¶Иэ№ъСЭТеЎ·ЎўЎ¶Л®д°ґ«Ў·ЎўЎ¶ємВҐГОЎ·КЗОТ№ъ№Еґъі¤ЖЄРЎЛµЦРµДµдРНґъ±нЈ¬±»іЖОЄЎ°ЛДґу№ЕµдГыЦшЎ±ДіЦРС§ОЄБЛЅвС§Йъ¶ФЛДґуГыЦшµДФД¶БЗйїцЈ¬ѕНЎ°ЛДґу№ЕµдГыЦшДг¶БНкБЛјёІїЎ±µДОКМвФЪИ«РЈС§ЙъЦРЅшРРБЛійСщµчІйЈ¬ёщѕЭµчІйЅб№ы»жЦЖіЙИзПВЙРІ»НкХыµДНіјЖНјЈ®
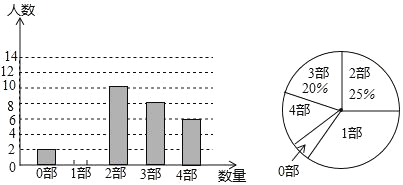
ЗлёщѕЭТФЙПРЕПўЈ¬ЅвѕцПВБРОКМв
(1)±ѕґОµчІйЛщµГКэѕЭµДЦЪКэКЗ____ІїЈ¬ЦРО»КэКЗ_____ІїЈ»
(2)ЙИРОНіјЖНјЦРЎ°4ІїЎ±ЛщФЪЙИРОµДФІРДЅЗОЄ_____¶ИЈ»
(3)ЗлЅ«МхРОНіјЖНјІ№ідНкХыЈ»
(4)Г»УР¶Б№эЛДґу№ЕµдГыЦшµДБЅГыС§ЙъЧј±ёґУЦРёчЧФЛж»ъСЎФсТ»ІїАґФД¶БЈ¬ЗуЛыГЗЗЎєГСЎЦРН¬Т»ГыЦшµДёЕВКЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
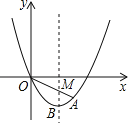
ЎѕМвДїЎїТСЦЄЈєИзНјЈ¬ФЪЖЅГжЦ±ЅЗЧш±кПµxOyЦРЈ¬ЕЧОпПЯyЈЅax2+bxЈЁaЎЩ0Ј©ѕ№эµгAЈЁ6Ј¬©Ѓ3Ј©Ј¬¶ФіЖЦбКЗЦ±ПЯxЈЅ4Ј¬¶ҐµгОЄBЈ¬OAУлЖд¶ФіЖЦбЅ»УЪµгMЈ¬MЎўN№ШУЪµгB¶ФіЖЈ®
ЈЁ1Ј©ЗуХвМхЕЧОпПЯµД±нґпКЅєНµгBµДЧш±кЈ»
ЈЁ2Ј©БЄЅбONЎўANЈ¬ЗуЎчOANµДГж»эЈ»
ЈЁ3Ј©µгQФЪxЦбЙПЈ¬ЗТФЪЦ±ПЯxЈЅ4УТІаЈ¬µ±ЎПANQЈЅ45ЎгК±Ј¬ЗуµгQµДЧш±кЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪЎ°УЕРгґ«НіОД»ЇЅшРЈФ°Ў±»о¶ЇЦРЈ¬С§РЈјЖ»®ГїЦЬ¶юПВОзµЪИэЅЪїОК±јдїЄХ№ґЛПо»о¶ЇЈ¬ДвїЄХ№»о¶ЇПоДїОЄЈєјфЦЅЈ¬ОдКхЈ¬Кй·ЁЈ¬ЖчАЦЈ¬ТЄЗуЖЯДкј¶С§ЙъИЛИЛІОјУЈ¬ІўЗТГїИЛЦ»ДЬІОјУЖдЦРТ»По»о¶ЇЈ®ЅМОсґ¦ФЪёГРЈЖЯДкј¶С§ЙъЦРЛж»ъійИЎБЛ100ГыС§ЙъЅшРРµчІйЈ¬Іў¶ФґЛЅшРРНіјЖЈ¬»жЦЖБЛИзНјЛщКѕµДМхРОНіјЖНјєНЙИРОНіјЖНјЈЁѕщІ»НкХыЈ©Ј®
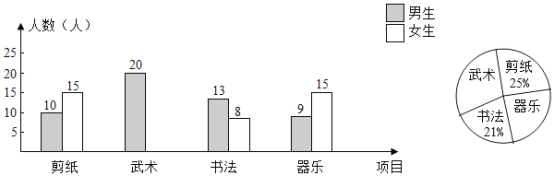
ЗлЅвґрПВБРОКМвЈє
ЈЁ1Ј©ЗлІ№И«МхРОНіјЖНјєНЙИРОНіјЖНјЈ»
ЈЁ2Ј©ФЪІОјУЎ°јфЦЅЎ±»о¶ЇПоДїµДС§ЙъЦРЈ¬ДРЙъЛщХјµД°Щ·Ц±ИКЗ¶аЙЩЈї
ЈЁ3Ј©ИфёГРЈЖЯДкј¶С§Йъ№ІУР500ИЛЈ¬Зл№АјЖЖдЦРІОјУЎ°Кй·ЁЎ±ПоДї»о¶ЇµДУР¶аЙЩИЛЈї
ЈЁ4Ј©С§РЈЅМОсґ¦ТЄґУХвР©±»µчІйµДЕ®ЙъЦРЈ¬Лж»ъійИЎТ»ИЛБЛЅвѕЯМеЗйїцЈ¬ДЗГґХэєГійµЅІОјУЎ°ЖчАЦЎ±»о¶ЇПоДїµДЕ®ЙъµДёЕВККЗ¶аЙЩЈї

Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com