
【题目】已知:关于x的方程![]()
(1)求证:m取任何值时,方程总有实根.
(2)若二次函数![]() 的图像关于y轴对称.
的图像关于y轴对称.
a、求二次函数![]() 的解析式
的解析式
b、已知一次函数![]() ,证明:在实数范围内,对于同一x值,这两个函数所对应的函数值
,证明:在实数范围内,对于同一x值,这两个函数所对应的函数值![]() 均成立.
均成立.
(3)在(2)的条件下,若二次函数![]() 的象经过(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值
的象经过(-5,0),且在实数范围内,对于x的同一个值,这三个函数所对应的函数值![]() 均成立,求二次函数
均成立,求二次函数![]() 的解析式.
的解析式.
【答案】(1)证明见解析;(2)a、y1=x2-1;b、证明见解析;(3)![]() .
.
【解析】
(1)首先此题的方程并没有明确是一次方程还是二次方程,所以要分类讨论:
①m=0,此时方程为一元一次方程,经计算可知一定有实数根;
②m≠0,此时方程为二元一次方程,可表示出方程的根的判别式,然后结合非负数的性质进行证明.
(2)①由于抛物线的图象关于y轴对称,那么抛物线的一次项系数必为0,可据此求出m的值,从而确定函数的解析式;
②此题可用作差法求解,令y1-y2,然后综合运用完全平方式和非负数的性质进行证明.
(3)根据②的结论,易知y1、y2的交点为(1,0),由于y1≥y3≥y2成立,即三个函数都交于(1,0),结合点(-5,0)的坐标,可用a表示出y3的函数解析式;已知y3≥y2,可用作差法求解,令y=y3-y2,可得到y的表达式,由于y3≥y2,所以y≥0,可据此求出a的值,即可得到抛物线的解析式.
解:(1)分两种情况:
当m=0时,原方程可化为3x-3=0,即x=1; ∴m=0时,原方程有实数根;
当m≠0时,原方程为关于x的一元二次方程,
∵△=[-3(m-1)]2-4m(2m-3)=m2-6m+9=(m-3)2≥0,
∴方程有两个实数根;
综上可知:m取任何实数时,方程总有实数根;
(2)①∵关于x的二次函数y1=mx2-3(m-1)x+2m-3的图象关于y轴对称;
∴3(m-1)=0,即m=1;
∴抛物线的解析式为:y1=x2-1;
②∵y1-y2=x2-1-(2x-2)=(x-1)2≥0,
∴y1≥y2(当且仅当x=1时,等号成立);
(3)由②知,当x=1时,y1=y2=0,即y1、y2的图象都经过(1,0);
∵对应x的同一个值,y1≥y3≥y2成立,
∴y3=ax2+bx+c的图象必经过(1,0),
又∵y3=ax2+bx+c经过(-5,0),
∴y3=a(x-1)(x+5)=ax2+4ax-5a;
设y=y3-y2=ax2+4ax-5a-(2x-2)=ax2+(4a-2)x+(2-5a);
对于x的同一个值,这三个函数对应的函数值y1≥y3≥y2成立,
∴y3-y2≥0,
∴y=ax2+(4a-2)x+(2-5a)≥0;
根据y1、y2的图象知:a>0,
∴y最小=![]() ≥0
≥0
∴(4a-2)2-4a(2-5a)≤0, ∴(3a-1)2≤0,
而(3a-1)2≥0,只有3a-1=0,解得a= ![]() ,
,
∴抛物线的解析式为:![]()


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
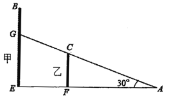
【题目】如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物一部分(把汽车看成一个点),这时视线与公路夹角为30°;
(1)汽车行驶到什么位置时,司机刚好看不到甲建筑物?请在图中标出这个D点;
(2)若CF的高度40米,当刚好看不到甲建筑物时,司机的视线与与公路夹角为45°,请问汽车行驶了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某环卫公司承包了市区两个片区道路的清扫任务,需要购买某厂家A,B两种型号的马路清扫车,购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元;购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元.
(1)求这两种马路清扫车的单价;
(2)恰逢该厂举行30周年庆,决定对这两种马路清扫车开展促销活动,具体方案如下:购买A型马路清扫车按原价的八折销售,购买B型马上清扫车不超过10辆时按原价销售,超过10辆的部分按原价的七折销售.设购买x辆A种马路清扫车需要y1元,购买x(x>0)个B型马路清扫车需要y2元,分别求出y1,y2关于x的函数关系式;
(3)若该公司承包的道路清扫面积为118000m2,每辆A型马路清扫车每天清扫5000m2,每辆B型马路清扫车每天清扫6000m2,公司准备购买20辆马路清扫车,且B型马路清扫车的数量大于10.请你帮该公司设计出最省钱的购买方案.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据2019年莆田市初中毕业升学体育考试内容要求,甲、乙、丙在某节体育课他们各自随机分别到篮球场A处进行篮球运球绕杆往返训练或到足球场B处进行足球运球绕杆训练,三名学生随机选择其中的一场地进行训练.
(1)用列表法或树形图表示出的所用可能出现的结果;
(2)求甲、乙、丙三名学生在同一场地进行训练的概率;
(3)求甲、乙、丙三名学生中至少有两人在B处场地进行训练的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
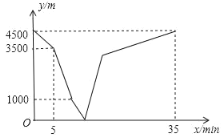
【题目】小雪和小松分别从家和图书馆出发,沿同一条笔直的马路相向而行.小雪开始跑步,中途在某地改为步行,且步行的速度为跑步速度的一半,小雪先出发5分钟后,小松才骑自行车匀速回家.小雪到达图书馆恰好用了35分钟.两人之间的距离y(m)与小雪离开出发地的时间x(min)之间的函数图象如图所示,则当小松刚到家时,小雪离图书馆的距离为____米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②9a+3b+c=0;③若点
;②9a+3b+c=0;③若点![]() ,点
,点![]() 是此函数图象上的两点,则
是此函数图象上的两点,则![]() ;④
;④![]() .其中正确的个数( )
.其中正确的个数( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,其中记载:“今有甲、乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八。问甲、乙二人原持钱各几何?”译文:“甲,乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文,如果乙得到甲所有钱的![]() ,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
,那么乙也共有钱48文,问甲、乙二人原来各有多少钱?”
查看答案和解析>>
科目:初中数学 来源: 题型:
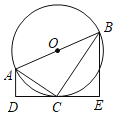
【题目】如图,AB是⊙O的直径,直线DE与⊙O相切于点C,过A,B分别作AD⊥DE,BE⊥DE,垂足为点D,E,连接AC,BC,若AD=![]() ,CE=3,则
,CE=3,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() πC.
πC.![]() πD.
πD.![]() π
π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com