
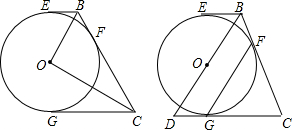
分析 (1)如图1中,根据切线长定理以及平行线的性质即可证明.
(2)如图2中,连接OC交FG于N,作FM⊥CD于M.由FG∥BD,得$\frac{FG}{BD}$=$\frac{CF}{CB}$=$\frac{CN}{OC}$=$\frac{4}{5}$,设CN=4k,OC=5k,想办法求出FM、CM即可解决问题.
解答 (1)证明: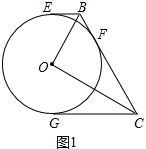 如图1中,∵BE、BC、CG是⊙O切线,
如图1中,∵BE、BC、CG是⊙O切线,
∴∠OBE=∠OBF,∠OCF=∠OCG,
∵EB∥CG,
∴∠EBC+∠GCB=180°,
∴2∠OBC+2∠OCB=180°,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∴OB⊥OC.
(2)解:如图2中,连接OC交FG于N,作FM⊥CD于M,则OF⊥CF.
∵CG=CF,∠OCG=∠OCF,
∴OC⊥FG,∴OC⊥BD,
∴FG∥BD,
∴$\frac{FG}{BD}$=$\frac{CF}{CB}$=$\frac{CN}{OC}$=$\frac{4}{5}$,设CN=4k,OC=5k,
∴ON=k,
∵OF2=ON•OC,CF2=CN•CO,FN2=ON•CN,
∴OF=$\sqrt{5}$k,CF=CG=2$\sqrt{5}$k,FN=2k,
∵$\frac{1}{2}$FG•CN=$\frac{1}{2}$•CG•FM,
∴FM=$\frac{8\sqrt{5}}{5}$k,
∴CM=$\sqrt{C{F}^{2}-F{M}^{2}}$=$\sqrt{(2\sqrt{5}k)^{2}-(\frac{8\sqrt{5}}{5}k)^{2}}$=$\frac{6\sqrt{5}}{5}$k,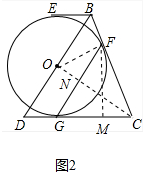
∴tan∠BCD=$\frac{FM}{CM}$=$\frac{\frac{8\sqrt{5}}{5}k}{\frac{6\sqrt{5}}{5}k}$=$\frac{4}{3}$.
点评 本题考查切线的性质、切线长定理、平行线分线段成比例定理、勾股定理等知识,解题的关键是添加辅助线构造直角三角形,记住射影定理的应用,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
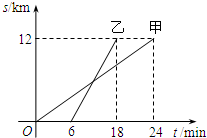 如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,则每分钟乙比甲多行驶的路程为( )
如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程s(km)随时间t(min)变化的函数图象,则每分钟乙比甲多行驶的路程为( )| A. | 1.5千米 | B. | 2千米 | C. | 0.5千米 | D. | 1千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
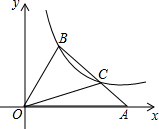 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,且tan∠BAO=$\frac{1}{2}$,OC是△OAB的中线,点B在第一象限,且其纵坐标为3,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,且tan∠BAO=$\frac{1}{2}$,OC是△OAB的中线,点B在第一象限,且其纵坐标为3,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com