
【题目】如图,矩形ABCD中,BC=4,将矩形ABCD绕点C顺时针旋转得到矩形A'B'C'D',此时点B'恰好落在边AD上.
(1)画出旋转后的图形;
(2)连接B'B,若∠AB'B=75°,求旋转角及AB长.

【答案】(1)答案见解析;(2)旋转角是30°,AB长为2.
【解析】
(1)先找到对应点,顺次连接得出旋转后的图形即可求解;
(2)连接B′B,作B′E⊥BC于E,根据三角形内角和定理可求∠ABB′,根据余角的定义可求∠CBB′,根据等腰三角形的性质和三角形内角和定理可求∠BCB′,根据含30°的直角三角形的性质求得B′E,即可求解.
(1)如图所示:
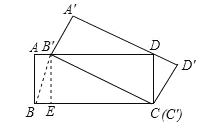
(2)连接B'B,作B'E⊥BC于E.
∵∠AB'B=75°,∴∠ABB'=15°,∴∠CBB'=75°.
∵CB=CB'=4,∴∠CBB'=∠CB'B=75°,∴∠BCB'=180°75°75°=30°,
∴B'E=![]() CB'=2,∴AB=2;
CB'=2,∴AB=2;
故旋转角是30°,AB长2.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
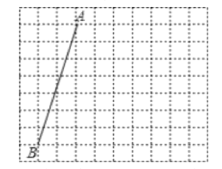
【题目】如图,方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。
(1)在图中画一个以AB为腰的等腰三角形△ABC点C在小正方形的顶点上,且tan∠B=3;
(2)在图中画一个以AB为底的等腰三角形△ABD点D在小正方形的项点上,且△ABD是锐角三角形。连接CD,请直接写出线段CD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
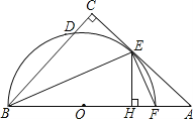
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EF=![]() ,求AF长.
,求AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国际无烟日”来临之际,小明就公众对在餐厅吸烟的态度进行了调查,并将调查结果制作成如图所示的统计图,请你根据图中信息回答:

(1)被调查者中,不吸烟者赞成在餐厅彻底禁烟的人数是 .
(2)被调查者中,希望在餐厅设立吸烟室的人数是 .
(3)求被调查者中赞成在餐厅彻底禁烟的频率.
(4)眉山市现有人口约380万,根据图中信息估计眉山市现有人口中赞成在餐厅彻底禁烟的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y = x2+bx+c过点A (-1,2),且关于y轴对称,点C与点B(a,0)(a>1)关于原点对称,直线AC交抛物线于点D.
(1)求此抛物线的解析式;
(2)连接OA,BD,当OA//BD时,求a的值;
(3)若直线AC交抛物线![]() 于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.
于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
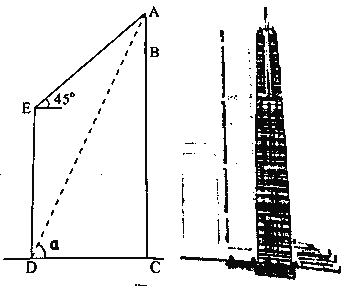
【题目】如图,长沙九龙仓国际金融中心主楼![]() 高达
高达![]() ,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼
,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼![]() 高
高![]() ,为了测量高楼
,为了测量高楼![]() 上发射塔
上发射塔![]() 的高度,在楼
的高度,在楼![]() 底端
底端![]() 点测得
点测得![]() 的仰角为α,
的仰角为α,![]() ,在顶端E测得A的仰角为
,在顶端E测得A的仰角为![]() ,求发射塔
,求发射塔![]() 的高度.
的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
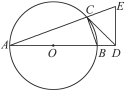
【题目】如图,已知点D在⊙O的直径AB延长线上,点C在⊙O上,过点D作ED⊥AD,与AC的延长线相交于点E,且CD=DE.
(1)求证:CD为⊙O的切线;
(2)若AB=12,且BC=CE时,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com