
二次函数y=(x-2m)2+1,当m<x<m+1时,y随x的增大而减小,则m的取值范围是__________.
m>1 【解析】由条件可知二次函数对称轴为x=2m,且开口向上,由二次函数的性质可知在对称轴的左侧时y随x的增大而减小,可求得m+1<2m,即m>1. 故答案为:m>1.科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:单选题
如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )
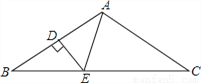
A. 80° B. 60° C. 50° D. 40°
D 【解析】首先利用三角形的内角和定理和等腰三角形的性质∠B,利用线段垂直平分线的性质易得AE=BE,∠BAE=∠B. 【解析】 ∵AB=AC,∠BAC=100°,∴∠B=∠C=(180°﹣100°)÷2=40°,∵DE是AB的垂直平分线,∴AE=BE,∴∠BAE=∠B=40°, 故选D.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:解答题
一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
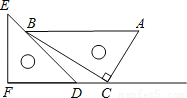
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,□ABCD的两个顶点B,D都在抛物线y= x2+bx+c上,且OB=OC,AB=5,tan∠ACB=
x2+bx+c上,且OB=OC,AB=5,tan∠ACB= .
.
(1)求抛物线的解析式;
(2)在抛物线上是否存在点E,使以A,C,D,E为顶点的四边形是菱形?若存在,请求出点E的坐标;若不存在,请说明理由.
(3)动点P从点A出发向点D运动,同时动点Q从点C出发向点A运动,运动速度都是每秒1个单位长度,当一个点到达终点时另一个点也停止运动,运动时间为t(秒).当t为何值时,△APQ是直角三角形?

查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,在△ABC中,正方形EDCF的三个顶点E,D,F都在三角形的边上,另一个顶点C与三角形的顶点重合,且AC=4,BC=6,求ED的长.

查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:单选题
如图,在Rt△ABC中,CD是斜边AB上的高,∠A≠45°,则下列比值中不等于sinA的是( )

A. 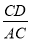 B.
B.  C.
C. 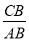 D.
D. 
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:单选题
一元二次方程x2﹣6x﹣5=0配方可变形为( )
A. (x﹣3)2=14 B. (x﹣3)2=4 C. (x+3)2=14 D. (x+3)2=4
A 【解析】试题分析:x2﹣6x﹣5=0,把方程的常数项移到右边得,x2﹣6x=5,方程两边都加上32得,x2﹣6x+9=5+9,所以(x﹣3)2=14,故答案选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版七年级数学上册:第5章 一元一次方程 单元测试卷 题型:单选题
方程-2x+3=0的解是( )
A. x= B. x=-
B. x=- C. x=
C. x= D. x=-
D. x=-
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县九年级(上)期末数学试卷(五四学制) 题型:填空题
如图,在⊙O中,弦AB=8,M是弦AB上的动点,且OM的最小值为3.则⊙O的半径为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com