
分析 先将$\frac{1}{{x}^{2}-x}$-$\frac{x-2}{{x}^{2}-2x+1}$÷$\frac{x-2}{x-1}$进行化简,然后将x的值代入求解即可.
解答 解:$\frac{1}{{x}^{2}-x}$-$\frac{x-2}{{x}^{2}-2x+1}$÷$\frac{x-2}{x-1}$
=$\frac{1}{{x}^{2}-x}$-$\frac{x-2}{(x-1)^{2}}$÷$\frac{x-2}{x-1}$
=$\frac{1}{{x}^{2}-x}$-$\frac{1}{x-1}$
=$\frac{1}{x(x-1)}$-$\frac{x}{x(x-1)}$
=$\frac{1-x}{x(x-1)}$
=-$\frac{1}{x}$.
∵x=-$\frac{1}{2}$,
∴原式=-$\frac{1}{x}$=2.
点评 本题考查了分式的化简求值,解答本题的关键在于将$\frac{1}{{x}^{2}-x}$-$\frac{x-2}{{x}^{2}-2x+1}$÷$\frac{x-2}{x-1}$进行化简,然后将x的值代入求解.


科目:初中数学 来源: 题型:解答题
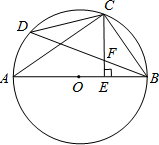 如图,AB是⊙O的直径,C是$\widehat{BD}$的中点,CE⊥AB于点E,BD交CE于点F.
如图,AB是⊙O的直径,C是$\widehat{BD}$的中点,CE⊥AB于点E,BD交CE于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
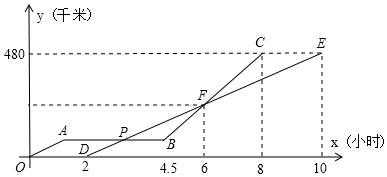
 将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )
将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )| A. | 18150 | B. | -18150 | C. | 18141 | D. | -18141 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
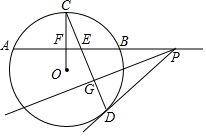 如图,在⊙O中,OC⊥AB于点F,弦CD交弦AB于点E,线段ED的垂直平分线GP交AB延长线于点P,连结PD.
如图,在⊙O中,OC⊥AB于点F,弦CD交弦AB于点E,线段ED的垂直平分线GP交AB延长线于点P,连结PD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+b}{2}$ | B. | $\frac{a+b}{11}$ | C. | $\frac{5a+6b}{11}$ | D. | $\frac{1}{2}$($\frac{a}{5}$+$\frac{b}{6}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
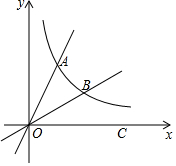 如图所示,已知函数y=$\frac{k}{x}$的图象与直线OA交于点A(1,$\sqrt{3}$),函数图象上一点B,x正半轴上的任意一点C,OB平分∠AOC.
如图所示,已知函数y=$\frac{k}{x}$的图象与直线OA交于点A(1,$\sqrt{3}$),函数图象上一点B,x正半轴上的任意一点C,OB平分∠AOC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com