练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．如图，直线a∥b，将三角尺的直角顶点放在直线b上，∠1=35°，求∠2的度数．

    分析 根据平角的定义求出∠3，再根据两直线平行，同位角相等可得∠2=∠3．

    解答 解：如图，∵∠1=35°，
    ∴∠3=180°-35°-90°=55°，
    ∵a∥b，
    ∴∠2=∠3=55°．

    点评 本题考查了平行线的性质，熟记性质并准确识图是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    4．已知∠A=60°，则∠A的补角是（　　）
    A．160°B．120°C．60°D．30°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．“2016年县球类运动会”的赛事共有三项：A．篮球，B．排球，C．乒乓球．小明和小刚参加了该项赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组．
    （1）小明被分配到“篮球”项目组的概率为$\frac{1}{3}$；
    （2）用树状图或列表法求小明和小刚被分配到不同项目组的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．用反证法证明“∠A≥60°”时，应假设∠A＜60°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查，调查的项目有：公共汽车、小车、摩托车、自行车、其它（每位同学仅选一项）．根据调查结果绘制了如下不完整的频数分布表和扇形统计图：
    交通方式频数（人数）频率
    公共汽车m0.25
    小车240.20
    摩托车36n
    自行车180.15
    其它120.10
    请根据图表信息解答下列问题：
    （1）本次共抽样调查120个学生；
    （2）填空：频数分布表中的m=30，n=0.3；
    （3）在扇形统计图中，请计算出“摩托车”所在的扇形的圆心角的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交直线DC于点F．
    （1）如图1，当点G在BC边上时，显然$\frac{DC}{DF}$=1，此时$\frac{AD}{AB}$=2．
    （2）如图2，当点G在矩形ABCD内部时，①若$\frac{AD}{AB}$=$\sqrt{2}$时，求$\frac{DC}{DF}$的值；②若$\frac{DC}{DF}$=k时，求$\frac{AD}{AB}$的值．
    （3）当点G在矩形ABCD外部且$\frac{DC}{DF}$=k，则$\frac{AD}{AB}$的值为$\frac{2\sqrt{k}}{k}$ （请直接写出结论即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．△ABC是⊙O的内接三角形，BC=$\sqrt{3}$．
    （1）如图1，若AC是⊙O的直径，∠BAC=60°，延长BA到点D，使得DA=$\frac{1}{2}$BA，过点D作直线l⊥BD，垂足为点D，请将图形补充完整，判断直线l和⊙O的位置关系并说明理由．
    （2）如图2，∠B=120°，点D是优弧$\widehat{AC}$的中点，DE∥BC交BA延长线于点E，BE=2，请将图形补充完整并求AB的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知，在Rt△ABC中，∠ACB=90°，请利用直角三角形全等的HL判定定理，求作Rt△DEF，使Rt△DEF≌Rt△ABC．

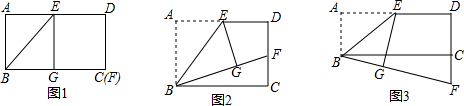
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．下列说法中，不正确的是（　　）
    A．2是（-2）2的算术平方根B．±2是（-2）2的平方根
    C．-2是（-2）2的算术平方根D．-2是（-2）3的立方根

    查看答案和解析>>

    同步练习册答案