
如图所示,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC为直角三角形,通过测量得到AC长160米,BC长128米,问从点A穿过湖到点B的距离是
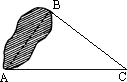
[ ]
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:044
如图所示,为了测量某湖的宽AB,在A,B两处找出两个标志点,然后在岸边找到一点O,沿AO方向确定一点D,作CD平行于AB,使C点与B,O在同一条直线上,这时测得AO=42.5 m,OD=3 m,CD=4.13 m,试求出湖宽AB.(精确到 0.1 m)

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 ,AN为独木舟船头A到船底的距离,为了计算
,AN为独木舟船头A到船底的距离,为了计算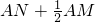 的值,小赵所在的科技小组进行了热烈的讨论:
的值,小赵所在的科技小组进行了热烈的讨论: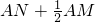 的值.
的值.
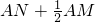 =________.
=________.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |

| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com