
”¾ĢāÄæ”æĪ»ÓŚŗÓÄĻŹ”µĒ·āŹŠ¾³ÄŚµÄŌŖ“ś¹ŪŠĒĢØ£¬ŹĒÖŠ¹śĻÖ“ę×īŌēµÄĢģĪÄĢØ£¬Ņ²ŹĒŹĄ½ēĪÄ»ÆŅŲśÖ®Ņ»£®
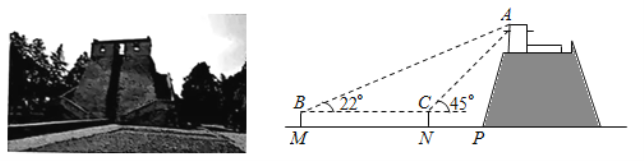
ijŠ£ŹżŃ§ÉēĶŵÄĶ¬Ń§ĆĒŹ¹ÓĆ¾ķ³ßŗĶ×ŌÖĘµÄ²ā½ĒŅĒ²āĮæ¹ŪŠĒĢصÄøß¶Č£®ČēĶ¼ĖłŹ¾£¬ĖūĆĒŌŚµŲĆęŅ»ĢõĖ® Ę½²½µĄ![]() ÉĻ¼ÜÉč²ā½ĒŅĒ£¬ĻČŌŚµć
ÉĻ¼ÜÉč²ā½ĒŅĒ£¬ĻČŌŚµć![]() “¦²āµĆ¹ŪŠĒĢØ×īøßµć
“¦²āµĆ¹ŪŠĒĢØ×īøßµć![]() µÄŃö½ĒĪŖ
µÄŃö½ĒĪŖ![]() £¬Č»ŗóŃŲ
£¬Č»ŗóŃŲ![]() ·½ĻņĒ°½ų
·½ĻņĒ°½ų![]() µ½“ļµć
µ½“ļµć![]() “¦£¬²āµĆµć
“¦£¬²āµĆµć![]() µÄŃö½ĒĪŖ
µÄŃö½ĒĪŖ![]() £®²ā½ĒŅĒµÄø߶ČĪŖ
£®²ā½ĒŅĒµÄø߶ČĪŖ![]() £¬
£¬
![]() Ēó¹ŪŠĒĢØ×īøßµć
Ēó¹ŪŠĒĢØ×īøßµć![]() ¾ąĄėµŲĆęµÄø߶Č(½į¹ū¾«Č·µ½
¾ąĄėµŲĆęµÄø߶Č(½į¹ū¾«Č·µ½![]() £®²Īæ¼Źż¾Ż£ŗ
£®²Īæ¼Źż¾Ż£ŗ ![]() )£»
)£»
![]() ”°¾°µć¼ņ½é”±ĻŌŹ¾£¬¹ŪŠĒĢصÄø߶ČĪŖ
”°¾°µć¼ņ½é”±ĻŌŹ¾£¬¹ŪŠĒĢصÄø߶ČĪŖ![]() £¬Ēė¼ĘĖć±¾“Ī²āĮæ½į¹ūµÄĪó²ī£¬²¢Ģį³öŅ»Ģõ¼õŠ”Īó²īµÄŗĻĄķ»Æ½ØŅ飮
£¬Ēė¼ĘĖć±¾“Ī²āĮæ½į¹ūµÄĪó²ī£¬²¢Ģį³öŅ»Ģõ¼õŠ”Īó²īµÄŗĻĄķ»Æ½ØŅ飮
”¾“š°ø”æ£Ø1£©12.3m£»£Ø2£©0.3m£¬¶ą“Ī²āĮ棬ĒóĘ½¾łÖµ
”¾½āĪö”æ
£Ø1£©¹żµćA×÷AE”ĶMN½»MNµÄŃÓ³¤ĻßÓŚµćE£¬½»BCµÄŃÓ³¤ĻßÓŚµćD£¬øł¾ŻĢõ¼žÖ¤³öĖıߊĪBMNCĪŖ¾ŲŠĪ”¢ĖıߊĪCNEDĪŖ¾ŲŠĪ”¢Čż½ĒŠĪACDÓėČż½ĒŠĪABD¾łĪŖÖ±½ĒČż½ĒŠĪ£¬ÉčADµÄ³¤ĪŖxm£¬ŌņCD=AD=xm£¬BD=BC+CD=£Ø16+x£©m£¬ŌŚRt”÷ABDÖŠ£¬½āÖ±½ĒČż½ĒŠĪĒóµĆADµÄ³¤¶Č£¬ŌŁ¼ÓÉĻDEµÄ³¤¶Č¼“æÉ£»
£Ø2£©øł¾Ż£Ø1£©ÖŠĖćµÄŹż¾ŻŗĶŹµ¼Źøß¶Č¼ĘĖćĪó²ī£¬½ØŅéŹĒ¶ą“Ī²āĮæĒóĘ½¾łÖµ£®
½ā£ŗ£Ø1£©ČēĶ¼£¬¹żµćA×÷AE”ĶMN½»MNµÄŃÓ³¤ĻßÓŚµćE£¬½»BCµÄŃÓ³¤ĻßÓŚµćD£¬
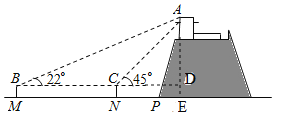
ÉčADµÄ³¤ĪŖxm£¬
”ßAE”ĶME£¬BC”ĪMN£¬
”ąAD”ĶBD£¬”ĻADC=90”ć£¬
”ß”ĻACD=45”ć£¬
”ąCD=AD=xm£¬BD=BC+CD=£Ø16+x£©m£¬
ÓÉĢāŅ×µĆ£¬ĖıߊĪBMNCĪŖ¾ŲŠĪ£¬
”ßAE”ĶME£¬
”ąĖıߊĪCNEDĪŖ¾ŲŠĪ£¬
”ąDE=CN=BM=![]() £¬
£¬
ŌŚRt”÷ABDÖŠ£¬![]() £¬
£¬
½āµĆ£ŗ![]() £¬
£¬
¼“AD=10.7m£¬AE=AD+DE=10.7+1.6=12.3m£¬
“š£ŗ¹ŪŠĒĢØ×īøßµć![]() ¾ąĄėµŲĆęµÄø߶ČĪŖ12.3m£®
¾ąĄėµŲĆęµÄø߶ČĪŖ12.3m£®
£Ø2£©±¾“Ī²āĮæ½į¹ūµÄĪó²īĪŖ£ŗ12.6-12.3=0.3m£¬
¼õŠ”Īó²īµÄŗĻĄķ»Æ½ØŅé£ŗ¶ą“Ī²āĮ棬ĒóĘ½¾łÖµ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
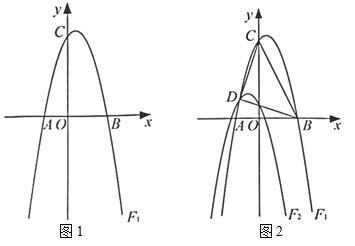
”¾ĢāÄæ”æČēĶ¼1ĖłŹ¾£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Å×ĪļĻß![]() Óė
Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() ŗĶµć
ŗĶµć![]() £¬Óė
£¬Óė![]() Öį½»ÓŚµć
Öį½»ÓŚµć![]() £®
£®
£Ø1£©ĒóÅ×ĪļĻß![]() µÄ±ķ“ļŹ½£»
µÄ±ķ“ļŹ½£»
£Ø2£©ČēĶ¼2£¬½«Å×ĪļĻß![]() ĻČĻņ×óĘ½ŅĘ1øöµ„Ī»£¬ŌŁĻņĻĀĘ½ŅĘ3øöµ„Ī»£¬µĆµ½Å×ĪļĻß
ĻČĻņ×óĘ½ŅĘ1øöµ„Ī»£¬ŌŁĻņĻĀĘ½ŅĘ3øöµ„Ī»£¬µĆµ½Å×ĪļĻß![]() £¬ČōÅ×ĪļĻß
£¬ČōÅ×ĪļĻß![]() ÓėÅ×ĪļĻß
ÓėÅ×ĪļĻß![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬
£¬![]() £¬
£¬![]() £®
£®
¢ŁĒóµć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
¢ŚÅŠ¶Ļ![]() µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Å×ĪļĻß![]() ÉĻŹĒ·ń“ęŌŚµć
ÉĻŹĒ·ń“ęŌŚµć![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬Čō“ęŌŚ£¬Ēó³öµć
ĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬Čō“ęŌŚ£¬Ēó³öµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
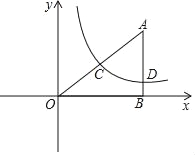
”¾ĢāÄæ”æČēĶ¼£¬Rt”÷ABOŌŚÖ±½Ē×ų±źĻµÖŠ£¬AB”ĶxÖįÓŚµćB£¬AO=10£¬sin”ĻAOB=![]() £®
£®
£Ø1£©Čō·“±ČĄżŗÆŹży=![]() £Øx£¾0£©µÄĶ¼Ļó¾¹żAOµÄÖŠµćC£¬ĒókµÄÖµ£»
£Øx£¾0£©µÄĶ¼Ļó¾¹żAOµÄÖŠµćC£¬ĒókµÄÖµ£»
£Ø2£©ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬Čō·“±ČĄżŗÆŹży=![]() £Øx£¾0£©µÄĶ¼ĻóÓėAB½»ÓŚµćD£¬µ±µćC£¬DĪ»ÓŚÖ±Ļßl£ŗy=©x+bµÄŅģ²ąŹ±£¬ĒóbµÄȔֵ·¶Ī§£»
£Øx£¾0£©µÄĶ¼ĻóÓėAB½»ÓŚµćD£¬µ±µćC£¬DĪ»ÓŚÖ±Ļßl£ŗy=©x+bµÄŅģ²ąŹ±£¬ĒóbµÄȔֵ·¶Ī§£»
£Ø3£©ČōµćD¹ŲÓŚyÖįµÄ¶Ō³ĘµćĪŖE£¬µ±·“±ČĄżŗÆŹży=![]() µÄĶ¼ĻóŗĶĻ߶ĪAEÓŠ¹«¹²µćŹ±£¬Ö±½ÓŠ“³ökµÄȔֵ·¶Ī§£®
µÄĶ¼ĻóŗĶĻ߶ĪAEÓŠ¹«¹²µćŹ±£¬Ö±½ÓŠ“³ökµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¾ÅÄź¼¶Ņ»°ąŃūĒė![]() ”¢
Ӣ![]() Ӣ
Ӣ![]() Ӣ
Ӣ![]() Ӣ
”¢![]() ĪåĪ»ĘĄĪƶŌ¼×”¢ŅŅĮ½Ī»Ķ¬Ń§µÄ²ÅŅÕ±ķŃŻ“ņ·Ö£¬²¢×éÖÆČ«°ą50ĆūĶ¬Ń§¶ŌĮ½ČĖĆńŅā²āĘĄĶ¶Ę±£¬»ęÖĘĮĖČēĻĀµÄ“ņ·Ö±ķŗĶ²»ĶźÕūµÄĢõŠĪĶ³¼ĘĶ¼£ŗ
ĪåĪ»ĘĄĪƶŌ¼×”¢ŅŅĮ½Ī»Ķ¬Ń§µÄ²ÅŅÕ±ķŃŻ“ņ·Ö£¬²¢×éÖÆČ«°ą50ĆūĶ¬Ń§¶ŌĮ½ČĖĆńŅā²āĘĄĶ¶Ę±£¬»ęÖĘĮĖČēĻĀµÄ“ņ·Ö±ķŗĶ²»ĶźÕūµÄĢõŠĪĶ³¼ĘĶ¼£ŗ
ĪåĪ»ĘĄĪƵēņ·Ö±ķ
A | B | C | D | E | |
¼× | 89 | 91 | 93 | 94 | 86 |
ŅŅ | 88 | 87 | 90 | 98 | 92 |
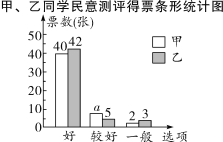
²¢ĒóµĆĮĖĪåĪ»ĘĄĪƶŌ¼×Ķ¬Ń§²ÅŅÕ±ķŃŻĖł“ņ·ÖŹżµÄĘ½¾ł·ÖŗĶÖŠĪ»Źż£ŗ
![]() £Ø·Ö£©£»ÖŠĪ»ŹżŹĒ91·Ö.
£Ø·Ö£©£»ÖŠĪ»ŹżŹĒ91·Ö.
£Ø1£©ĒóĪåĪ»ĘĄĪƶŌŅŅĶ¬Ń§²ÅŅÕ±ķŃŻĖł“ņ·ÖŹżµÄĘ½¾ł·ÖŗĶÖŠĪ»Źż£»
£Ø2£©![]() ________£¬²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
________£¬²¢²¹Č«ĢõŠĪĶ³¼ĘĶ¼£»
£Ø3£©ĪŖĮĖ“Ó¼×”¢ŅŅĮ½ČĖ֊ֻє°Ī³öŅ»ČĖČ„²Ī¼ÓŅÕŹõ½ŚŃŻ³ö£¬°ą¼¶ÖʶØĮĖČēĻĀµÄŃ”°Ī¹ęŌņ£ŗ
Ń”°Ī¹ęŌņ£ŗŃ”°Ī×ŪŗĻ·Ö×īøßµÄĶ¬Ń§²Ī¼ÓŅÕŹõ½ŚŃŻ³ö.ĘäÖŠ£¬×ŪŗĻ·Ö£½²ÅŅÕ·Ö![]() ²āĘĄ·Ö
²āĘĄ·Ö![]() £»
£»
²ÅŅÕ·Ö£½ĪåĪ»ĘĄĪÆĖł“ņ·ÖŹżÖŠČ„µōŅ»øö×īøß·ÖŗĶŅ»øö×īµĶ·Ö£¬ŌŁĖćĘ½¾ł·Ö£»²āĘĄ·Ö£½”°ŗĆ”±Ę±Źż”Į2·Ö£«”°½ĻŗĆ”±Ę±Źż”Į1·Ö£«”°Ņ»°ć”±Ę±Źż”Į0·Ö
¢Łµ±![]() Ź±£¬Ķعż¼ĘĖćĖµĆ÷Ӧє°ĪÄÄĪ»Ķ¬Ń§Č„²Ī¼ÓŅÕŹõ½ŚŃŻ³ö£æ
Ź±£¬Ķعż¼ĘĖćĖµĆ÷Ӧє°ĪÄÄĪ»Ķ¬Ń§Č„²Ī¼ÓŅÕŹõ½ŚŃŻ³ö£æ
¢ŚĶعż¼ĘĖćĖµĆ÷![]() µÄÖµ²»ÄÜŹĒ¶ąÉŁ£æ
µÄÖµ²»ÄÜŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚČ«ĢåĄöĖ®ČĖĆńµÄŬĮ¦ĻĀ£¬ĪŅŹŠ½ĖĆšĮÓVĄąĖ®”°ŗÓµĄĒåÓŁ”±¹¤³ĢČ”µĆĮĖ½×¶ĪŠŌ³É¹ū£¬Čē±ķŹĒČ«ŹŠŹ®øöĻŲ£ØŹŠ”¢Ēų£©Öø±źČĪĪńŹżµÄĶ³¼Ę±ķ£»ČēĶ¼ŹĒ½ŲÖ¹2017Äź3ŌĀ31ČÕŗĶ½ŲÖ¹5ŌĀ4ČÕ£¬Č«ŹŠŹ®øöĻŲ£ØŹŠ”¢Ēų£©Öø±źČĪĪńĄŪ¼ĘĶź³ÉŹżµÄĶ³¼ĘĶ¼£®
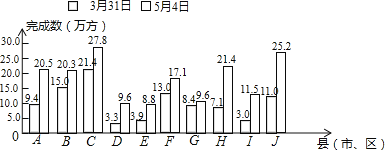
Č«ŹŠŹ®øöĻŲ£ØŹŠ”¢Ēų£©Öø±źČĪĪńŹżĶ³¼Ę±ķ
ĻŲ£ØŹŠ”¢Ēų£© | ČĪĪńŹż£ØĶņ·½£© |
A | 25 |
B | 25 |
C | 20 |
D | 12 |
E | 13 |
F | 25 |
G | 16 |
H | 25 |
I | 11 |
J | 28 |
ŗĻ¼Ę | 200 |
£Ø1£©½ŲÖ¹3ŌĀ31ČÕ£¬Ķź³É½ų¶Č£ØĶź³É½ų¶Č£½ĄŪ¼ĘĶź³ÉŹż”ĀČĪĪńŹż”Į100%£©×īæģ”¢×īĀżµÄĻŲ£ØŹŠ”¢Ēų£©·Ö±šŹĒÄÄŅ»øö£æ
£Ø2£©Ēó½ŲÖ¹5ŌĀ4ČÕČ«ŹŠµÄĶź³É½ų¶Č£»
£Ø3£©Ēė½įŗĻĶ¼±ķŠÅĻ¢ŗĶŹż¾Ż·ÖĪö£¬¶Ō¢ńĻŲĶź³ÉÖø±źČĪĪńµÄŠŠ¶Æ¹ż³ĢŗĶ³É¹ū½ųŠŠĘĄ¼Ū£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
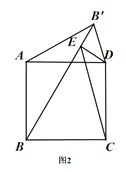
”¾ĢāÄæ”æ½«Õż·½ŠĪ![]() µÄ±ß
µÄ±ß![]() Čʵć
Čʵć![]() ÄꏱÕėŠż×ŖÖĮ
ÄꏱÕėŠż×ŖÖĮ![]() £¬¼ĒŠż×Ŗ½ĒĪŖ
£¬¼ĒŠż×Ŗ½ĒĪŖ![]() £®Į¬½Ó
£®Į¬½Ó![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() “¹Ö±ÓŚÖ±Ļß
“¹Ö±ÓŚÖ±Ļß![]() £¬“¹×ćĪŖµć
£¬“¹×ćĪŖµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬
£¬
![]() ČēĶ¼1£¬µ±
ČēĶ¼1£¬µ±![]() Ź±£¬
Ź±£¬![]() µÄŠĪדĪŖ £¬Į¬½Ó
µÄŠĪדĪŖ £¬Į¬½Ó![]() £¬æÉĒó³ö
£¬æÉĒó³ö![]() µÄÖµĪŖ £»
µÄÖµĪŖ £»

![]() µ±
µ±![]() ĒŅ
ĒŅ![]() Ź±£¬
Ź±£¬
¢Ł![]() ÖŠµÄĮ½øö½įĀŪŹĒ·ńČŌČ»³ÉĮ¢?Čē¹ū³ÉĮ¢£¬Ēė½ö¾ĶĶ¼2µÄĒéŠĪ½ųŠŠÖ¤Ć÷£»Čē¹ū²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£»
ÖŠµÄĮ½øö½įĀŪŹĒ·ńČŌČ»³ÉĮ¢?Čē¹ū³ÉĮ¢£¬Ēė½ö¾ĶĶ¼2µÄĒéŠĪ½ųŠŠÖ¤Ć÷£»Čē¹ū²»³ÉĮ¢£¬ĒėĖµĆ÷ĄķÓÉ£»
¢Śµ±ŅŌµć![]() ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬ĒėÖ±½ÓŠ“³ö
ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪŹ±£¬ĒėÖ±½ÓŠ“³ö![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijµŲŅ»ÖÖÉĢĘ·µÄŠčĒóĮæ![]() £ØĶņ¼ž£©ÓėÉĢĘ·¼Ūøń
£ØĶņ¼ž£©ÓėÉĢĘ·¼Ūøń![]() £ØŌŖ/¼ž£©“ęŌŚŅ»“ĪŗÆŹż¹ŲĻµ£¬ĒŅ¼ŪøńĪŖ10ŌŖ/¼žŹ±£¬ŠčĒóĮæŹĒ50Ķņ¼ž£»µ±¼ŪøńŹĒ20ŌŖ/¼žŹ±£¬ŠčĒóĮæŹĒ40Ķņ¼ž£¬øĆÉĢĘ·µÄ¹©Ó¦Įæ
£ØŌŖ/¼ž£©“ęŌŚŅ»“ĪŗÆŹż¹ŲĻµ£¬ĒŅ¼ŪøńĪŖ10ŌŖ/¼žŹ±£¬ŠčĒóĮæŹĒ50Ķņ¼ž£»µ±¼ŪøńŹĒ20ŌŖ/¼žŹ±£¬ŠčĒóĮæŹĒ40Ķņ¼ž£¬øĆÉĢĘ·µÄ¹©Ó¦Įæ![]() £ØĶņ¼ž£©ÓėÉĢĘ·µÄ¼Ūøń
£ØĶņ¼ž£©ÓėÉĢĘ·µÄ¼Ūøń![]() £ØŌŖ/¼ž£©µÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
£ØŌŖ/¼ž£©µÄŗÆŹż¹ŲĻµČēĶ¼ĖłŹ¾£®
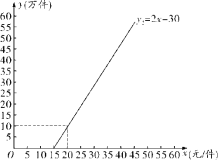
£Ø1£©Ēó![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄŗÆŹż¹ŲĻµŹ½£¬²¢ŌŚ×ų±źĻµÖŠ»³öĖüµÄĶ¼Ļó£»
µÄŗÆŹż¹ŲĻµŹ½£¬²¢ŌŚ×ų±źĻµÖŠ»³öĖüµÄĶ¼Ļó£»
£Ø2£©ŅŖŹ¹ÉĢĘ·¼ŪøńĻą¶ŌĪČ¶Ø£¬Šč±£³Ö¹©Ó¦ĮæÓėŠčĒóĮæµÄ“óÖĀĘ½ŗā£Ø¼ņ³Ę¹©ŠčĘ½ŗā£©£¬ÄćČĻĪŖÉĢĘ·µÄ¼Ūøń¶ØŌŚĆ漞¶ąÉŁŌŖŹ±£¬¹©Šč×īĘ½ŗā£»ÉĢĘ·¼ŪøńŹĒĆ漞¶ąÉŁŌŖŹ±£¬¹©“óÓŚĒó£æ
£Ø3£©µ±ŹŠ³”¹©Ó¦Įæ“óÓŚŠčĒóĮæµÄ![]() Ź±£¬Õžø®¾Ķ»į·¢³öŌ¤¾Æ£¬ÄĒĆ“Õžø®·¢³öŌ¤¾ÆŹ±£¬ÉĢĘ·µÄ×īµĶ¼ŪøńŹĒĆ漞¶ąÉŁŌŖ£æ£Ø¾«Č·µ½ŌŖ£©
Ź±£¬Õžø®¾Ķ»į·¢³öŌ¤¾Æ£¬ÄĒĆ“Õžø®·¢³öŌ¤¾ÆŹ±£¬ÉĢĘ·µÄ×īµĶ¼ŪøńŹĒĆ漞¶ąÉŁŌŖ£æ£Ø¾«Č·µ½ŌŖ£©
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com