练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】解方程
    （1）2x﹣1=3
    （2）2（3﹣x）=﹣4x+5
    （3） = +1．

    【答案】
    （1）解：移项合并得：2x=4，

    解得：x=2


    （2）解：去括号得：6﹣2x=﹣4x+5，

    移项合并得：2x=﹣1，

    解得：x=﹣


    （3）解：去分母得：3x﹣3=4x+2+12，

    移项合并得：﹣x=17，

    解得：x=﹣17


    【解析】（1）方程移项合并，把x系数化为1，即可求出解；（2）方程去括号，移项合并，把x系数化为1，即可求出解；（3）方程去分母，去括号，移项合并，把x系数化为1，即可求出解．
    【考点精析】认真审题，首先需要了解解一元一次方程的步骤(先去分母再括号，移项变号要记牢．同类各项去合并，系数化“1”还没好．求得未知须检验，回代值等才算了)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线y=﹣x2+bx+c经过A（﹣1，0），B（4，0）两点，与y轴相交于点C，连结BC，点P为抛物线上一动点，过点P作x轴的垂线l，交直线BC于点G，交x轴于点E．

    （1）求抛物线的表达式；

    （2）当P位于y轴右边的抛物线上运动时，过点C作CF⊥直线l，F为垂足，当点P运动到何处时，以P，C，F为顶点的三角形与△OBC相似？并求出此时点P的坐标；

    （3）如图2，当点P在位于直线BC上方的抛物线上运动时，连结PC，PB，请问△PBC的面积S能否取得最大值？若能，请求出最大面积S，并求出此时点P的坐标，若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于任意实数a、b，定义：a◆b=a2+ab+b2．若方程（x◆2）-5=0的两根记为m、n，则m2＋n2=______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC，点D为AC上一点，且BD=BC．将△BCD沿直线BD折叠后，点C落在AB上的点E处，若AE=DE，则∠A的度数为 ．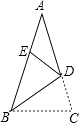

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】由于雾霾天气频发，市场上防护口罩出现热销，某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只，且所有产品当月全部售出，原料成本、销售单价及工人生产提成如表：

    甲

    乙

    原料成本

    12

    8

    销售单价

    18

    12

    生产提成

    1

    0.8

    （1）若该公司五月份的销售收入为300万元，求甲、乙两种型号的产品分别是多少万只？

    （2）公司实行计件工资制，即工人每生产一只口罩获得一定金额的提成，如果公司六月份投入总成本（原料总成本+生产提成总额）不超过239万元，应怎样安排甲、乙两种型号的产量，可使该月公司所获利润最大？并求出最大利润（利润=销售收入﹣投入总成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知直线l1：y=x+3与x轴交于点A，与y轴交于点B，与直线l2：y=﹣ x交于点P．直线l3：y=﹣ x+4与x轴交于点C，与y轴交于点D，与直线l1交于点Q，与直线l2交于点R．

    （1）点A的坐标是 ， 点B的坐标是 ， 点P的坐标是；
    （2）将△POB沿y轴折叠后，点P的对应点为P′，试判断点P′是否在直线l3上，并说明理由；
    （3）求△PQR的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：x3ya+1是关于x，y的六次单项式，试求下列代数式的值：
    （1）a2+2a+1
    （2）（a+1）2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解答题。
    （1）定义新运算：对于任意有理数a，b，都有a⊕b=a（a﹣b）+1，等式右边是通常的加法、减法及乘法运算，比如，数字2和5在该新运算下结果为﹣5．计算如下：
    2⊕5=2×（2﹣5）+1
    =2×（﹣3）+1
    =﹣6+1
    =﹣5
    求（﹣2）⊕3的值；
    （2）对于有理数a、b，若定义运算：ab= （﹣4）3的值等于
    （3）请你定义一种新运算，使得数字﹣4和6在你定义的新运算下结果为20．写出你定义的新运算．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】方程x（x+2）＝﹣x（x+2）的根是（　　）

    A. x1＝0，x2＝2B. x1＝0，x2＝﹣2C. x＝0D. x＝2

    查看答案和解析>>

    同步练习册答案