

���� ��1����ͼ1�У���ֱ��EF���O�����ڵ�K����FM��AD��M�����ı���CDMF�Ǿ��Σ���֪ED=EK=2-t��FC=FK=2t���Ƴ�EF=2+t��EM=2-t-2t=2-3t��FM=CD=2����Rt��EFM�У�����EF2=FM2+EM2���г����̼��ɽ�����⣻
��2������ͼ2�У���t=$\frac{4}{5}$ʱ��AE=$\frac{4}{5}$��CF=$\frac{8}{5}$��ED=2-$\frac{4}{5}$=$\frac{6}{5}$�����ı���CDEF��ֱ�����Σ�����OP=$\frac{DE+CF}{2}$�����OP���ٸ������ĵ����ʼ��ɽ�����⣮Q�ǡ�PDC�����ģ��ó�PQ=$\frac{2}{3}$OP��
�������ʼλ��ʱ����ֹλ��ʱQO�ij����ɽ�����⣻
��� �⣺��1����ͼ1�У���ֱ��EF���O�����ڵ�K����FM��AD��M�����ı���CDMF�Ǿ��Σ�
��֪ED=EK=2-t��FC=FK=2t��
��EF=2+t��EM=2-t-2t=2-3t��FM=CD=2��
��Rt��EFM����EF2=FM2+EM2��
�ࣨ2+t��2=22+��2-3t��2��
��t=$\frac{1}{4}$��1����������
��t=$\frac{1}{4}$sʱ��ֱ��EF���O���У�
��2������ͼ2�У���t=$\frac{4}{5}$ʱ��AE=$\frac{4}{5}$��CF=$\frac{8}{5}$��ED=2-$\frac{4}{5}$=$\frac{6}{5}$
���ı���CDEF��ֱ�����Σ�
�֡�EP=PF��DO=OC��
��OP=$\frac{DE+CF}{2}$=$\frac{7}{5}$��
��Q�ǡ�PDC�����ģ�
��PQ=$\frac{2}{3}$OP=$\frac{14}{15}$��
����ͼ3�У�
����F�˶�����B�غ�ʱ��OP=$\frac{3}{2}$��OQ=$\frac{1}{3}$OP=$\frac{1}{2}$��
����ʼλ��ʱ��OQ=$\frac{1}{3}$��
���Q���˶�·��Ϊ$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{6}$��
���� ���⿼��Բ�ۺ��⡢���ߵ��ж������ʡ����ɶ�����ֱ�����ε����ʣ������ε����ĵ����ʵ�֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ֱ�������ν�����⣬���������ѧ֪ʶ������⣬�����п�ѹ���⣮


 �����ҵ��ٿ���������������ϵ�д�
�����ҵ��ٿ���������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��E��?ABCD��DC��һ�㣬����ֻ��һ��û�п̶ȵ�ֱ�ߣ���AB����ȷ��һ��F��ʹ��BF=DE������ʾ��ͼ������Ҫ˵����ͼ���̣�
��ͼ��E��?ABCD��DC��һ�㣬����ֻ��һ��û�п̶ȵ�ֱ�ߣ���AB����ȷ��һ��F��ʹ��BF=DE������ʾ��ͼ������Ҫ˵����ͼ���̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����Rt��ABC�У���C=90�㣬��A=30�㣬DΪAB�е㣬DE��AC��E��AB=8����DE�ij���Ϊ��������
��ͼ����Rt��ABC�У���C=90�㣬��A=30�㣬DΪAB�е㣬DE��AC��E��AB=8����DE�ij���Ϊ��������| A�� | 1 | B�� | 2 | C�� | 4 | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
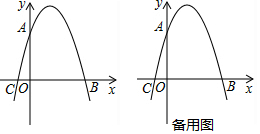
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���������ABCDE�У���A+��B+��E=����DP��CP�ֱ�ƽ�֡�EDC����BCD�����P�Ķ����ǣ�������
��ͼ���������ABCDE�У���A+��B+��E=����DP��CP�ֱ�ƽ�֡�EDC����BCD�����P�Ķ����ǣ�������| A�� | 90��+$\frac{1}{2}$�� | B�� | $\frac{1}{2}��$-90�� | C�� | $\frac{1}{2}��$ | D�� | 540��$-\frac{1}{2}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ����ƽ���ı��� | B�� | һ�������� | ||
| C�� | һ���Ǿ��� | D�� | һ���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC��AB=AC����DΪBC���е㣬AE�ǡ�BAC��ǵ�ƽ���ߣ�DE��AB��AE��E�����ı���ADCE����״�Ǿ��Σ�
��ͼ���ڡ�ABC��AB=AC����DΪBC���е㣬AE�ǡ�BAC��ǵ�ƽ���ߣ�DE��AB��AE��E�����ı���ADCE����״�Ǿ��Σ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com