
 的图像经过点
的图像经过点 和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
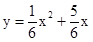
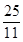 ,0).
,0).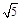 ,由CB∥x轴得到∠ABC=∠BAP,再分类讨论:当△ABC∽△BAP;当△ABC∽△PAB,然后利用比例线段求AP的长,从而确定P点坐标.
,由CB∥x轴得到∠ABC=∠BAP,再分类讨论:当△ABC∽△BAP;当△ABC∽△PAB,然后利用比例线段求AP的长,从而确定P点坐标.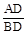 =2.
=2. 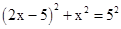 ,
, ,
,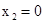 (不合题意,舍去).
(不合题意,舍去).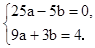 ,解这个方程组,得
,解这个方程组,得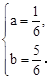
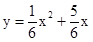
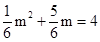 , 解得
, 解得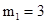 (不合题意,舍去),
(不合题意,舍去),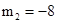 .
. .
.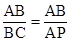 ,
,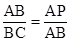 ,
, ,点P的坐标为(
,点P的坐标为(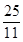 ,0).
,0).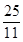 ,0).
,0).

科目:初中数学 来源:不详 题型:解答题
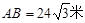 ,
,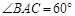 .设
.设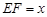 米,
米,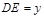 米.
米.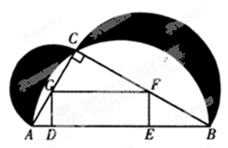
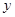 与
与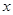 之间的函数解析式;
之间的函数解析式;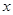 为何值时,矩形的面积最大?最大面积是多少?
为何值时,矩形的面积最大?最大面积是多少? 为何值时,矩形的面积等于两弯新月面积的
为何值时,矩形的面积等于两弯新月面积的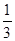 ?
?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 (千克)随销售单价
(千克)随销售单价 (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为: ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:
(元),解答下列问题: 与
与 的关系式;
的关系式; 取何值时,
取何值时, 的值最大?
的值最大?查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.向左平移1个单位,再向上平移3各单位 |
| B.向左平移1个单位,再向下平移3个单位 |
| C.向右平移1个单位,再向上平移3个单位 |
| D.向右平移1个单位,再向下平移3个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com