
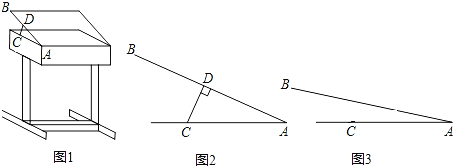
【题目】某课桌生产厂家研究发现,倾斜12°﹣24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.
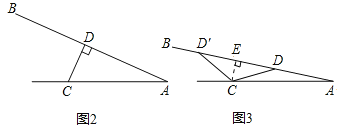
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长.
(2)如图3,当∠BAC=12°,求AD的长(结果保留根号).
[参考数据:sin24°=0.40,cos24°=0.91,tan24°=0.46,sin12°=0.20]
【答案】(1)12;(2)AD的长为(12![]() +6
+6![]() )cm或(12
)cm或(12![]() ﹣6
﹣6![]() )cm.
)cm.
【解析】
(1)在Rt△ACD中利用锐角三角函数关系得出sin24°=![]() ,代入数值计算即可求出CD的长;
,代入数值计算即可求出CD的长;
(2)过点C作CE⊥AB于点E,在Rt△ACE中利用锐角三角函数关系得出sin12°=![]() ,求出CE的长,再根据勾股定理求出DE,AE的长,进而得出AD的长.
,求出CE的长,再根据勾股定理求出DE,AE的长,进而得出AD的长.
(1)在Rt△ACD中,∵∠DAC=24°,∠ADC=90°,
∴sin24°=![]() ,
,
∴CD=ACsin24°=30×0.40=12cm;
∴此时支撑臂CD的长为12cm;
(2)如图,过点C作CE⊥AB于点E,
当∠BAC=12°时,
∴sin12°=![]() =
=![]() ,
,
∴CE=30×0.20=6cm,
∵CD=12cm,
∴DE=![]() =
=![]() =6
=6![]() cm,
cm,
∴AE=![]() =12
=12![]() cm,
cm,
∴AD的长为(12![]() +6
+6![]() )cm或(12
)cm或(12![]() ﹣6
﹣6![]() )cm.
)cm.


科目:初中数学 来源: 题型:
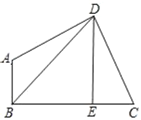
【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,DE⊥BC于E,连接BD,设AD=m,DC=n,BE=p,DE=q.
(1)若tanC=2,BE=3,CE=2,求点B到CD的距离;
(2)若m=n, BD=3![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图:过直线外一点作已知直线的平行线.
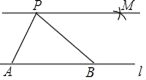
已知:如图,直线l与直线l外一点P.
求作:过点P与直线l平行的直线.

已知:如图,直线l与直线l外一点P.
求作:过点P与直线l平行的直线.

作法如下:
(1)在直线l上任取两点A、B,连接AP、BP;
(2)以点B为圆心,AP长为半径作弧,以点P为圆心,AB长为半径作弧,如图所示,两弧相交于点M;
(3)过点P、M作直线;
(4)直线PM即为所求.
(1)在直线l上任取两点A、B,连接AP、BP;
(2)以点B为圆心,AP长为半径作弧,以点P为圆心,AB长为半径作弧,如图所示,两弧相交于点M;
(3)过点P、M作直线;
(4)直线PM即为所求.

请回答:PM平行于l的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )
A. a≤﹣1或![]() ≤a<
≤a<![]() B.
B. ![]() ≤a<
≤a<![]()
C. a≤![]() 或a>
或a>![]() D. a≤﹣1或a≥
D. a≤﹣1或a≥![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.

(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长.
(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;
(3)如图2,在(1)的条件下,擦去折痕AO,线段OP,连结BP,动点M在线段AP⊥(点M与点F、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作DE⊥BD交BC的延长线于点E.
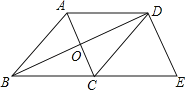
(1)求证:四边形ACED是平行四边形;
(2)若BD=4,AC=3,求cos∠CDE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们设计了一个重复抛掷的实验:全班48人分为8个小组,每组抛掷同一型号的一枚瓶盖300次,并记录盖面朝上的次数,下表是依次累计各小组的实验结果.
1组 | 1~2组 | 1~3组 | 1~4组 | 1~5组 | 1~6组 | 1~7组 | 1~8组 | |
盖面朝上次数 | 165 | 335 | 483 | 632 | 801 | 949 | 1122 | 1276 |
盖面朝上频率 | 0.550 | 0.558 | 0.537 | 0.527 | 0.534 | 0.527 | 0.534 | 0.532 |
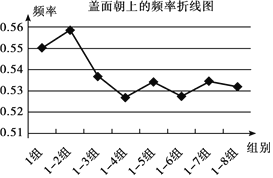
根据实验,你认为这一型号的瓶盖盖面朝上的概率为____,理由是:____.
查看答案和解析>>
科目:初中数学 来源: 题型:
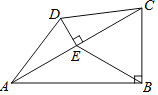
【题目】如图,在四边形ABCD中,∠ABC=90°,DE⊥AC于点E,且AE=CE,DE=5,EB=12.
(1)求AD的长;
(2)若∠CAB=30°,求四边形ABCD的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com