
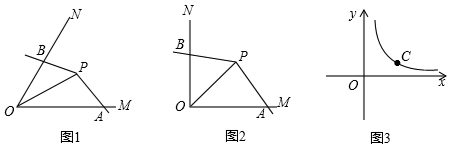
 如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.
如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,我们就把∠APB叫做∠MON的智慧角.分析 (1)由角平分线求出∠AOP=∠BOP=$\frac{1}{2}$∠MON=45°,再证出∠OAP=∠OPB,证明△AOP∽△POB,得出对应边成比例$\frac{OA}{OP}=\frac{OP}{OB}$,得出OP2=OA•OB,即可得出结论;
(2)设点C(a,b),则ab=3,过点C作CH⊥OA于H;分两种情况:
①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,BC=2CA不可能;当得A在x轴的正半轴上时;先求出$\frac{CA}{AB}=\frac{1}{3}$,由平行线得出△ACH∽△ABO,得出比例式:$\frac{CH}{OB}=\frac{AH}{OA}=\frac{CA}{AB}=\frac{1}{3}$,得出OB=3b,OA=$\frac{3}{2}$a,求出OA•OB=$\frac{27}{2}$,根据∠APB是∠AOB的智慧角,得出OP,即可得出点P的坐标;
②当点B在y轴的负半轴上时;由题意得出:AB=CA,由AAS证明△ACH≌△ABO,得出OB=CH=b,OA=AH=$\frac{1}{2}$a,得出OA•OB=$\frac{3}{2}$,求出OP,即可得出点P的坐标.
解答 (1)证明:∵∠MON=90°,P为∠MON的平分线上一点,
∴∠AOP=∠BOP=$\frac{1}{2}$∠MON=45°,
∵∠AOP+∠OAP+∠APO=180°,
∴∠OAP+∠APO=135°,
∵∠APB=135°,
∴∠APO+∠OPB=135°,
∴∠OAP=∠OPB,
∴△AOP∽△POB,
∴$\frac{OA}{OP}=\frac{OP}{OB}$,
∴OP2=OA•OB,
∴∠APB是∠MON的智慧角;
(2)设点C(a,b),则ab=3,
过点C作CH⊥OA于H;分两种情况:
①当点B在y轴正半轴上时;当点A在x轴的负半轴上时,如图2:
BC=2CA不可能;
当点A在x轴的正半轴上时,如图3:
∵BC=2CA,
∴$\frac{CA}{AB}=\frac{1}{3}$,
∵CH∥OB,
∴△ACH∽△ABO,
∴$\frac{CH}{OB}=\frac{AH}{OA}=\frac{AC}{AB}=\frac{1}{3}$,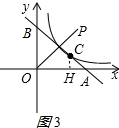
∴OB=3b,OA=$\frac{3}{2}$a,
∴OA•OB=$\frac{3}{2}$a•3b=$\frac{9ab}{2}$=$\frac{27}{2}$,
∵∠APB是∠AOB的智慧角,
∴OP=$\sqrt{OA•OB}=\sqrt{\frac{27}{2}}$=$\frac{3\sqrt{6}}{2}$,
∵∠AOB=90°,OP平分∠AOB,
∴点P到x,y轴的距离相等为$\frac{3\sqrt{3}}{2}$
∴点P的坐标为:($\frac{3\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{2}$);
②当点B在y轴的负半轴上时,如图4,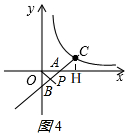
∵BC=2CA,
∴AB=CA,
在△ACH和△ABO中,$\left\{\begin{array}{l}{∠AHC=∠AOB}\\{∠BAO=∠CAH}\\{CA=AB}\end{array}\right.$
,∴△ACH≌△ABO(AAS),
∴OB=CH=b,OA=AH=$\frac{1}{2}$a,
∴OA•OB=$\frac{1}{2}$a•b=$\frac{3}{2}$,
∵∠APB是∠AOB的智慧角,
∴OP=$\sqrt{OA•OB}$=$\frac{\sqrt{6}}{2}$,
∵∠AOB=90°,OP平分∠AOB,
∴点P到x,y轴的距离相等为$\frac{\sqrt{3}}{2}$,
∴点P的坐标为:($\frac{\sqrt{3}}{2}$,-$\frac{\sqrt{3}}{2}$);
综上所述:点P的坐标为:($\frac{3\sqrt{3}}{2}$,$\frac{3\sqrt{3}}{2}$),或($\frac{\sqrt{3}}{2}$,-$\frac{\sqrt{3}}{2}$).
点评 此题是反比例函数综合题,主要考查了角平分线的性质、相似三角形的判定与性质、新定义以及运用、全等三角形的判定与性质等知识;本题难度较大,综合性强,特别是(3)中,需要通过作辅助线进行分类讨论,证明三角形相似和三角形全等才能得出结果.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题
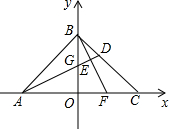 如图,在平面直角坐标系中,OA=OB=OC=6,点G的线段OB上的一个动点,连接AG并延长BC于点D.
如图,在平面直角坐标系中,OA=OB=OC=6,点G的线段OB上的一个动点,连接AG并延长BC于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
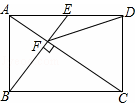 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有①②③⑤.
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$;⑤S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论有①②③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
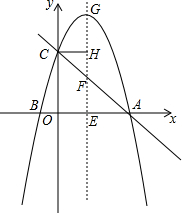 已知抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于点C,点B的坐标为(-1,0),过x轴上一点E作EG⊥x轴交抛物线于点G,交直线AC于点F.
已知抛物线y=ax2+bx+4与x轴交于A,B两点,与y轴交于点C,点B的坐标为(-1,0),过x轴上一点E作EG⊥x轴交抛物线于点G,交直线AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
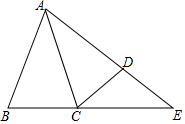 如图△ABC中,AB=AC=8,∠BAC=30°,现将△ABC绕点A逆时针旋转30°得到△ACD,延长AD、BC交于点E,则DE的长是4$\sqrt{3}$-4.
如图△ABC中,AB=AC=8,∠BAC=30°,现将△ABC绕点A逆时针旋转30°得到△ACD,延长AD、BC交于点E,则DE的长是4$\sqrt{3}$-4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8,半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3,将Rt△ABC绕点A顺时针旋转,设旋转角为α(0°≤α≤180°)
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,AB=8,半径为$\sqrt{3}$的⊙M与射线BA相切,切点为N,且AN=3,将Rt△ABC绕点A顺时针旋转,设旋转角为α(0°≤α≤180°)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com