
分析 过A作AG⊥BE于G,设AC、BD交于O,则AGBO是正方形,所以△AEG是直角三角形,又AG=AO=$\frac{1}{2}$AC=$\frac{1}{2}$AE,然后根据含30度角的直角三角形的性质即可求解.
解答 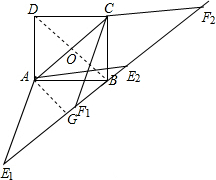 解:过A作AG⊥BE于G,设AC与BD相交于点O,如下图所示:
解:过A作AG⊥BE于G,设AC与BD相交于点O,如下图所示:
设AC,BD交于O,则AGBO是正方形,
∴AG=AO=$\frac{1}{2}$AC=$\frac{1}{2}$AE1,
又∵AG⊥GE1,
∴∠AE1B=30°.
∵CF∥AE,
∴∠CF1E1=150°,∠CF1B=30°,
∴CF1=AC=CF2,
∴CF1=CF2,
∴∠CF2E2=∠CF1B=30°
∴∠CFE=150°或∠CFE=30°.
故答案为150°或30°.
点评 本题考查正方形的性质,难度适中,解答本题要充分利用正方形的特殊性质,即对角线互相垂直、平分、相等.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
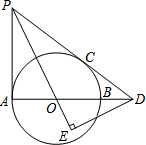 如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.
如图,AB是⊙O的直径,PA,PC分别与⊙O相切于点A,C,PC交AB的延长线于点D,DE⊥PO交PO的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交干点E,EC与AD相交于点F,过C点作CG∥AD,交BA的延长线于G,过A作BC的平行线交CG于H点.
在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,与AB相交干点E,EC与AD相交于点F,过C点作CG∥AD,交BA的延长线于G,过A作BC的平行线交CG于H点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com