
 如图,已知⊙O是锐角△ABC的外接圆,BE,CF分别是AC,AB边上的高,自垂足E,F分别作AB,AC的垂线,垂足为G,H,设EG与FH相交于K.
如图,已知⊙O是锐角△ABC的外接圆,BE,CF分别是AC,AB边上的高,自垂足E,F分别作AB,AC的垂线,垂足为G,H,设EG与FH相交于K.分析 (1)由于EG⊥AF,FH⊥AE,说明K是△AEF的垂心,所以只需证明AO垂直EF即可,也就是证∠AFE+∠BAP=90°,而B、F、E、C四点共圆是显然的,因此,只需证∠AFE+∠ACB=90°,而AO是半径,AO并延长交⊙O于点P,连接BP,则∠BPA=∠ACB,∠APB+∠BAP=90°,结论水落石出.
(2)由于题目没有告诉任何角度条件,那么直接进行角度的换算是行不通的了.注意到∠BAC处在直角三角形中,因此,只要求出∠BAC对应的三角函数值也能达到目的,也就只需求出$\frac{AF}{AC}$即可,问题转化为推导线段的比例关系,由此想到三角形相似;设BE、CF交于点L,则L为△ABC的垂心,连接AL,则AL⊥BC,连接BO并延长交⊙O于点M,连接CM、AM,过点O作ON⊥BC于N,△AFK∽△ACL、△BON∽△CAF是显然的,并且易证ON=$\frac{1}{2}$CM=$\frac{1}{2}$AL;由△AFK∽△ACL可得$\frac{AK}{AL}$=$\frac{AF}{AC}$;由△BON∽△CAF可得$\frac{ON}{OB}$=$\frac{AF}{AC}$,注意到ON=$\frac{1}{2}$CM=$\frac{1}{2}$AL,AO=BO=2AK,则$\frac{\frac{1}{2}AL}{2AK}$=$\frac{AF}{AC}$,将两式相乘即可求出$\frac{AF}{AC}$,即可得答案.
解答 解:(1)如图1,连接AO并延长交⊙O于点P,连接BP,设BE、CF交于点L,连接AL并延长交BC于点J,连接EF,
∵BE⊥AC,CF⊥AB,
∠BFC=∠BEC=90°,
∴B、F、E、C四点共圆,
∴∠AFE=∠ACB,
∵∠ACB=∠APB,
∴∠AFE=∠APB,
∵AP是直径,
∴∠ABP=90°,
∴∠APB+∠BAP=90°,
∴∠AFE+∠BAP=90°,
∴AO⊥EF,
∵FH⊥AE,EG⊥AF,EG与AF交于点K,
∴K为△AEF的垂心,
∴A、K、O三点共线;
(2)如图2,设BE、CF交于点L,则L为△ABC的垂心,连接AL,则AL⊥BC,连接BO并延长交⊙O于点M,连接CM、AM,过点O作ON⊥BC于N,
∵BM是直径,
∴MA⊥AB,
∵CF⊥AB,
∴CF∥MA,
同理AL∥CM,
∴四边形ALCM是平行四边形,
∴AL=CM,
∵ON⊥BC,BO=OM,
∴ON=$\frac{1}{2}$CM=$\frac{1}{2}$AL,
∵AL⊥BC,
∴∠LAC+∠ACB=90°,
∵∠BAP+∠APB=90,∠APB=∠ACB,
∴∠BAP=∠CAL,
∵∠AFH+∠BAC=∠ACF+∠BAC=90°,
∴AFH=∠ACF,
∴△AFK∽△ACL,
∴$\frac{AK}{AL}$=$\frac{AF}{AC}$,①
∵∠BON=$\frac{1}{2}$∠BOC=∠BAC,
∴△BON∽△CAF,
∴$\frac{ON}{OB}$=$\frac{AF}{AC}$,
∵ON=$\frac{1}{2}$CM=$\frac{1}{2}$AL,AO=BO=2AK,
∴$\frac{\frac{1}{2}AL}{2AK}$=$\frac{AF}{AC}$,②
①、②两式相乘可得:($\frac{AF}{AC}$)2=$\frac{1}{4}$,
∴$\frac{AF}{AC}$=$\frac{1}{2}$,即cos∠BAC=$\frac{1}{2}$,
∴∠BAC=60°.
点评 本题考查了三角形垂心的性质、三角形外接圆性质、圆周角与圆心角的性质、四点共圆的判定与性质、相似三角形的判定与性质,平行四边形的判定与性质、三角函数等众多的知识点,难度很大,是一道非常经典的平面几何竞赛题.本题的解答要求学生必须具备深厚的数学功底、敏锐的观察能力和几何直觉.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点O是坐标原点,A(0,6),AB=4$\sqrt{3}$,且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.
如图,在平面直角坐标系中,点O是坐标原点,A(0,6),AB=4$\sqrt{3}$,且∠OBA=60°,将△OAB沿直线AB翻折,得到△CAB,点O与点C对应.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
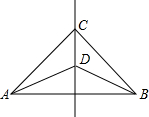 CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.
CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2100}{x}$×30=$\frac{1200}{36-x}$×20 | B. | $\frac{2100}{x}$=$\frac{1200}{36-x}$ | ||
| C. | $\frac{2100}{20x}$=$\frac{1200}{30(26-x)}$ | D. | $\frac{2100}{30x}=\frac{1200}{20(26-x)}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
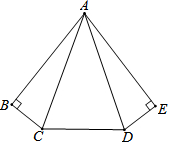 已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.
已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
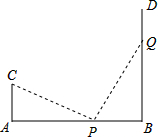 如图,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动3分钟后△CAP与△PQB全等.
如图,AB=9cm,CA⊥AB于A,DB⊥AB于B,且AC=3m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动3分钟后△CAP与△PQB全等.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=3,b=1 | B. | a=-3,b=1 | C. | a=3,b=-1 | D. | a=-3,b=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com