
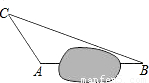
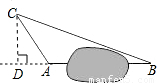
 解:如图,过C作CD⊥AB于D交BA的延长线于D.
解:如图,过C作CD⊥AB于D交BA的延长线于D.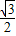 =15
=15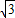 .
. AC=15.
AC=15.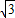 m,
m, =
= =65.
=65.

科目:初中数学 来源: 题型:
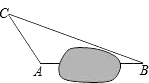 在一次综合实践活动中,同学们要测量某公园的人工湖两侧A、B两个凉亭之间的距离(如图)现测得AC=30m,BC=70m,∠CAB=120°,则A、B两个凉亭之间的距离为
在一次综合实践活动中,同学们要测量某公园的人工湖两侧A、B两个凉亭之间的距离(如图)现测得AC=30m,BC=70m,∠CAB=120°,则A、B两个凉亭之间的距离为查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•贵阳)在一次综合实践活动中,小明要测某地一座古塔AE的高度,如图,已知塔基AB的高为4m,他在C处测得塔基顶端B的仰角为30°,然后沿AC方向走5m到达D点,又测得塔顶E的仰角为50°.(人的身高忽略不计)
(2013•贵阳)在一次综合实践活动中,小明要测某地一座古塔AE的高度,如图,已知塔基AB的高为4m,他在C处测得塔基顶端B的仰角为30°,然后沿AC方向走5m到达D点,又测得塔顶E的仰角为50°.(人的身高忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com