
【题目】已知抛物线y1=x2+bx+c的顶点坐标为(﹣1,1),直线1的解析式为y2=2mx+3m2+4nm+4n2,且l与x轴、y轴分别交于A、B两点.
(1)求b、c的值;
(2)若函数y1+y2的图象与x轴始终有公共点,求直线l的解析式;
(3)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB为等腰角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)b的值为2,c的值为2;(2)当△PAB是等腰三角形时,点P坐标为(﹣1,4)或(﹣1,![]() )或(﹣1,﹣
)或(﹣1,﹣![]() )或(﹣1,2).
)或(﹣1,2).
【解析】
试题分析:(1)利用顶点坐标公式,待定系数法列出方程组即可解决问题.(2)根据△≥0,以及非负数的性质即可解决问题.(3)首先求出A、B坐标,分三种情形讨论即可①当BA=BP时,②当AB=AP时,③当PA=PB时.
试题解析:(1)∵抛物线y1=x2+bx+c的顶点坐标为(﹣1,1),
∴ ,解得:
,解得:![]() ,
,
∴b的值为2,c的值为2.
(2)y1+y2=x2+2x+2+2mx+3m2+4nm+4n2=x2+(2+2m)x+3m2+4nm+4n2+2,
∵函数y1+y2的图象与x轴始终有公共点,
∴△=(2+2m)2﹣4×1×(3m2+4nm+4n2+2)≥0,即﹣4(m﹣1)2﹣4(m+2n)2≥0.
∵(m﹣1)2≥0,(m+2n)2≥0,
∴m=1,n=﹣![]() ,
,
∴直线l的解析式为y=2x+2.
(3)如图,A(﹣1,0),B(0,2).AB=![]() =
=![]() ,对称轴x=﹣1,
,对称轴x=﹣1,
①当BA=BP时,可得P1(﹣1,4),
②当AB=AP时,可得P2(﹣1,![]() ),P3(﹣1,﹣
),P3(﹣1,﹣![]() ),
),
③当PA=PB时,可得P4(﹣1,2).
综上所述,当△PAB是等腰三角形时,点P坐标为(﹣1,4)或(﹣1,![]() )或(﹣1,﹣
)或(﹣1,﹣![]() )或(﹣1,2).
)或(﹣1,2).



科目:初中数学 来源: 题型:
【题目】下列说法中:①因为∠1与∠2是对顶角,所以∠1=∠2;②因为∠1与∠2是邻补角,所以∠1=∠2;③因为∠1与∠2不是对顶角,所以∠1≠∠2;④因为∠1与∠2不是邻补角,所以∠1+∠2≠180°.
其中正确的有(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条信息在一周内被转发了2180000次,将数据2180000用科学记数法表示为( )
A. 2.18×105 B. 2.18×106 C. 21.8×106 D. 21.8×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了认真贯彻教育部关于与开展“阳光体育”活动的文件精神,实施全国亿万学生每天集体锻炼一小时活动,吸引同学们走向操场、走进大自然、走到阳光下,积极参加体育锻炼,掀起校园内体育锻炼热潮,我市各学校结合实际情况举办了“阳光体育”系列活动,为了解“阳光体育”活动的落实情况,我市教育部门在红旗中学2000名学生中,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的活动),并将调查结果绘制成如下两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)参加调查的人数共有 人,在扇形统计图中,表示“C”的扇形的圆心角为 度;
(2)补全条形统计图,并计算扇形统计图中m的值;
(3)若要从该校喜欢“D”项目的学生中随机选择8名进行节目排练,则喜欢该项目的小丽同学被选中的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品的进价为 300 元,售价为 550 元.后来由于该商品积压,商店准备打折销售, 但要保证利润率为 10%,则该商品可打_____折.
查看答案和解析>>
科目:初中数学 来源: 题型:
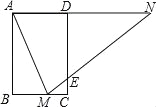
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E
(1)求证:△AMN是等腰三角形;
(2)求BMAN的最大值;
(3)当M为BC中点时,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
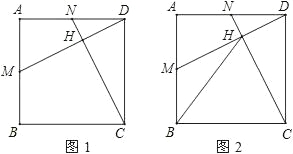
【题目】如图(1),点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.
(1)证明:①CN=DM;②CN⊥DM;
(2)设CN、DM的交点为H,连接BH,如图(2),求证:△BCH是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com