
分析 先由已知条件得出m+n=6,$m-n=4\sqrt{2}$,mn=1,再将m2n-mn2变形为mn(m-n),$\frac{m}{n}$+$\frac{n}{m}$变形为$\frac{{{{(m+n)}^2}-2mn}}{mn}$,整体代入即可求解.
解答 解:∵$m=3+2\sqrt{2}$,$n=3-2\sqrt{2}$,
∴m+n=6,$m-n=4\sqrt{2}$,mn=1,
∴(1)${m^2}n-m{n^2}=mn(m-n)=1×4\sqrt{2}=4\sqrt{2}$;
(2)$\frac{m}{n}+\frac{n}{m}=\frac{{{m^2}+{n^2}}}{mn}$=$\frac{{{{(m+n)}^2}-2mn}}{mn}$=34.
点评 考查了分母有理化,关键是由已知条件得出m+n=6,$m-n=4\sqrt{2}$,mn=1,注意整体思想的运用.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:解答题
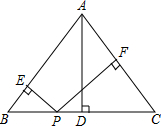 在△ABC中,AB=AC=10,BC=12,BC边上高AD=8,P为BC边上一动点,PE⊥AB于E,PF⊥AC于F.
在△ABC中,AB=AC=10,BC=12,BC边上高AD=8,P为BC边上一动点,PE⊥AB于E,PF⊥AC于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不等式的两边都加上(或减去)同一个整式,不等号的方向不变 | |
| B. | 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变 | |
| C. | 不等式的两边都乘以(或除以)同一个负数,不等号的方向改变 | |
| D. | 以上答案均不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h,有下列四种说法:①a•b=c•h;②a+b<c+h;③以a+b、h、c+h为边的三角形,是直角三角形;④$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$.其中正确的有( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,设AC=b,BC=a,AB=c,CD=h,有下列四种说法:①a•b=c•h;②a+b<c+h;③以a+b、h、c+h为边的三角形,是直角三角形;④$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com