
【题目】某铁路桥长1000米.现有一列火车从桥上匀速通过.测得火车从开始上桥到完全通过桥共用了1分钟(即从车头进入桥头到车尾离开桥尾),整个火车完全在桥上的时间为40秒.
(1)如果设这列火车的长度为x米,填写下表(不需要化简):
火车行驶过程 | 时间(秒) | 路程(米) | 速度(米/秒) |
完全通过桥 | 60 | ||
整列车在桥上 | 40 |
(2)求这列火车的长度.
科目:初中数学 来源: 题型:
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合)DE∥AB交AC于点F,CE∥AM,连结AE.
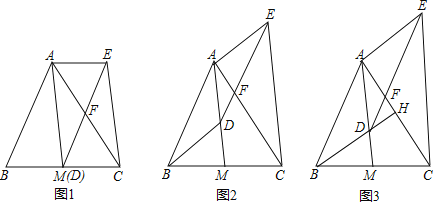
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM
①求∠CAM的度数;
②当FH=![]() , DM=4时,求DH的长.
, DM=4时,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
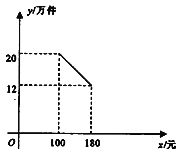
【题目】杰瑞公司成立之初投资1500万元购买新生产线生产新产品,此外,生产每件该产品还需要成本60元.按规定,该产品售价不得低于100元/件且不得超过180元/件,该产品销售量y(万件)与产品售价x(元)之间的函数关系如图所示.
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或者亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利达1340万元,若能,求出第二年产品售价;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,0是坐标原点,点A坐标为(2, 0),点B坐标为(0, b) (b>0), 点P是直线AB上位于第二象限内的一个动点,过点P作PC垂直于x轴于点C,记点P关于y轴的对称点为Q.
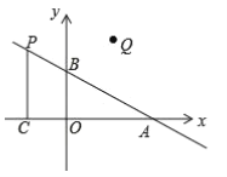
(1)当b=1时:①求直线AB相应的函数表达式:②若![]() ,求点P的坐标:
,求点P的坐标:
(2)设点P的横坐标为a,是否同时存在a、b,使得![]() 是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在长方形![]() 中,
中,![]() ,现将长方形
,现将长方形![]() 向上平移
向上平移![]() ,再向左平移
,再向左平移![]() 后到长方形
后到长方形![]() 的位置(
的位置(![]() 的对应点为
的对应点为![]() ,其它类似).
,其它类似).
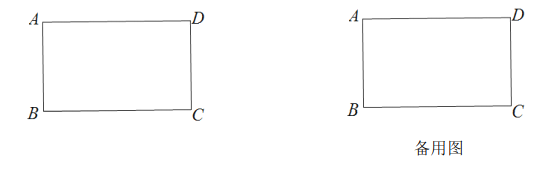
![]() 当
当![]() 时,请画出平移后的长方形
时,请画出平移后的长方形![]() ,并求出长方形
,并求出长方形![]() 与长方形
与长方形![]() 的重叠部分的面积.
的重叠部分的面积.
![]() 当
当![]() 满足什么条件时,长方形
满足什么条件时,长方形![]() 与长方形
与长方形![]() 有重叠部分(边与边叠合不算在内),请用
有重叠部分(边与边叠合不算在内),请用![]() 的代数式表示重叠部分的面积.
的代数式表示重叠部分的面积.
![]() 在平移的过程中,总会形成一个六边形
在平移的过程中,总会形成一个六边形![]() ,试用
,试用![]() 来表示六边形
来表示六边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
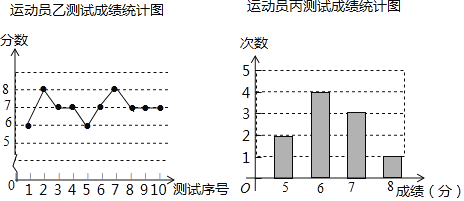
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:数轴上有![]() 、
、![]() 两点,分别对应的数为
两点,分别对应的数为![]() ,
,![]() ,已知
,已知![]() 与
与![]() 互为相反数,点
互为相反数,点![]() 为数轴上一动点,对应为
为数轴上一动点,对应为![]() .
.
(1)若点![]() 到点
到点![]() 和点
和点![]() 的距离相等,求点
的距离相等,求点![]() 对应的数;
对应的数;
(2)数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() 和点
和点![]() 的距离之和为5?若存在,请求出
的距离之和为5?若存在,请求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)当点![]() 以每分钟1个单位长度的速度从
以每分钟1个单位长度的速度从![]() 点向左运动,点
点向左运动,点![]() 以每分钟5个单位长度向左运动,点
以每分钟5个单位长度向左运动,点![]() 以每分钟20个单位长度的速度向左运动,问几分钟时点
以每分钟20个单位长度的速度向左运动,问几分钟时点![]() 到点
到点![]() 、点
、点![]() 的距离相等.
的距离相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.
(1)求证:△DOE≌△BOF.
(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com