
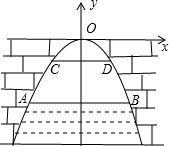
 如图所示建立的直角坐标系中,抛物线的解析式为y=-$\frac{1}{2}$x2,当涵洞水面宽AB为12米时,水面到拱桥顶点O的距离为18米.
如图所示建立的直角坐标系中,抛物线的解析式为y=-$\frac{1}{2}$x2,当涵洞水面宽AB为12米时,水面到拱桥顶点O的距离为18米. 科目:初中数学 来源: 题型:解答题
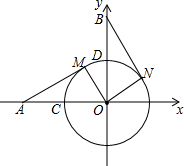 已知,如图坐标轴上点A(-4,0)、B(0,4),以点O为圆心,2为半径作⊙O与x轴的负半轴、y轴的正半轴分别交于点C、D,将扇形COD绕点O顺时针旋转α°得到扇形MON(点M与点C、点N与点D对应,其中0°≤α≤360°),连接AM、BN.
已知,如图坐标轴上点A(-4,0)、B(0,4),以点O为圆心,2为半径作⊙O与x轴的负半轴、y轴的正半轴分别交于点C、D,将扇形COD绕点O顺时针旋转α°得到扇形MON(点M与点C、点N与点D对应,其中0°≤α≤360°),连接AM、BN.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 10 | 5 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
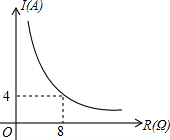 已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,如果以此蓄电池为电源的用电器限制电流不超过10A,那么此用电器的可变电阻为( )
已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,如果以此蓄电池为电源的用电器限制电流不超过10A,那么此用电器的可变电阻为( )| A. | 不小于3.2Ω | B. | 不大于3.2Ω | C. | 不小于12Ω | D. | 不大于12Ω |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com