
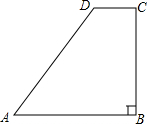
 如图,在直角梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形沿过B点的直线折叠,使A点恰好与D点重合,BE为折痕.
如图,在直角梯形ABCD中,∠DCB=90°,AB∥CD,AB=25,BC=24.将该梯形沿过B点的直线折叠,使A点恰好与D点重合,BE为折痕.分析 (1)取AD的中点,连接BE、BD,则△EBD为翻折后得到的三角形;
(2)过点D作DF⊥AB,垂足为F,由勾股定理先求得DC=7,从而可知AF=18,然后在△AFD中由勾股定理可求得AD=30.
解答 解:(1)如图1所示:
(2)如图所示:过点D作DF⊥AB,垂足为F.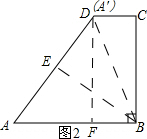
∵∠C=∠CBF=∠BFD=90°,
∴四边形BCDF为矩形.
∴DC=BF,DF=CB.
由翻折的性质可知:AB=DB=25.
在Rt△BDC中,由勾股定理可知:DC=$\sqrt{B{D}^{2}-B{C}^{2}}$=$\sqrt{2{5}^{2}-2{4}^{2}}$=7.
∴AF=18.
在Rt△ADF中,由勾股定理得:AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{1{8}^{2}+2{4}^{2}}$=30.
点评 本题主要考查的是翻折的性质、矩形的性质和判定、勾股定理的应用,求得DC、AF的长是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
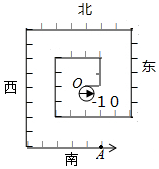 把一数轴折成如图所示,第1段为1个单位长度,第2段为2个单位长度,第3段为3个单位长度,…点O处有一个圆,圆上刻一指针,开始指针朝东,圆周为4个单位长度,圆紧贴数轴沿着数轴的正方向滚动,当圆与点A接触时,指针指向北(东、南、西、北),当圆与2015接触时,指针指向北(东、南、西、北).
把一数轴折成如图所示,第1段为1个单位长度,第2段为2个单位长度,第3段为3个单位长度,…点O处有一个圆,圆上刻一指针,开始指针朝东,圆周为4个单位长度,圆紧贴数轴沿着数轴的正方向滚动,当圆与点A接触时,指针指向北(东、南、西、北),当圆与2015接触时,指针指向北(东、南、西、北).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
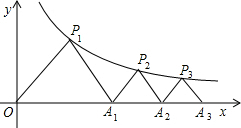 如图,△P1OA1,△P2A1A2,△P3A2A3…△PnAn-1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数$y=\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.则点P12的坐标是(4$\sqrt{3}$+2$\sqrt{11}$,4$\sqrt{3}$-2$\sqrt{11}$).
如图,△P1OA1,△P2A1A2,△P3A2A3…△PnAn-1An都是等腰直角三角形,点P1、P2、P3…Pn都在函数$y=\frac{4}{x}$(x>0)的图象上,斜边OA1、A1A2、A2A3…An-1An都在x轴上.则点P12的坐标是(4$\sqrt{3}$+2$\sqrt{11}$,4$\sqrt{3}$-2$\sqrt{11}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com