
【题目】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q. 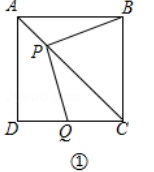
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
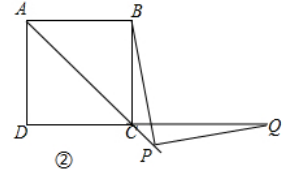
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
【答案】
(1)解:结论:PB=PQ,
理由:如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形.
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
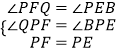 ,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)解:结论:PB=PQ.
理由:如图②,过P作PE⊥BC,PF⊥CD,垂足分别为E,F,
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
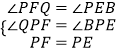 ,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
【解析】(1)结论:PB=PQ,如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.只要证明Rt△PQF≌Rt△PBE即可.(2)结论不变,证明方法类似.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE. 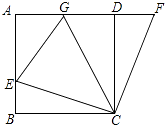
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般情况下 ![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得 ![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;
(3)若(m,n)是“相伴数对”,求代数式m﹣ ![]() ﹣[4m﹣2(3n﹣1)]的值.
﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2017年的“双11”网上促销活动中,淘宝网的交易额突破了350000 0000元,将数字3500000000科学记数法表示为______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“丝绸之路”经济带首个实体平台﹣﹣中哈物流合作基地在我市投入使用,其年最大装卸能力达410000标箱.其中“410000”用科学记数法表示为( )
A.0.41×106
B.4.1×105
C.41×104
D.4.1×104
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com