
【题目】已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
(1)当点C,E,F在直线AB的同侧时(如图①所示),试说明∠BOE=2∠COF.
(2)当点C与点E,F在直线AB的两侧时(如图②所示),(1)中的结论是否仍然成立?请给出你的结论,并说明理由.

【答案】(1)∠BOE=2∠COF(2)∠BOE=2∠COF仍成立
【解析】
(1)先设![]() ,得出
,得出![]() ,再根据角平分线的定义得出
,再根据角平分线的定义得出![]() ,从而得出
,从而得出![]() 的数量关系;
的数量关系;
(2)设![]() ,求出
,求出![]() ,推出
,推出![]() 、
、![]() 即可得出答案.
即可得出答案.
(1)设∠COF=α,
则∠EOF=90°-α.
因为OF是∠AOE的平分线,
所以∠AOE=2∠EOF=2(90°-α)=180°-2α.
所以∠BOE=180°-∠AOE=180°-(180°-2α)=2α.
所以∠BOE=2∠COF.
(2)∠BOE=2∠COF仍成立.
理由:设∠AOC=β,
则∠AOE=90°-β,
又因为OF是∠AOE的平分线,
所以∠AOF=![]() .
.
所以∠BOE=180°-∠AOE=180°-(90°-β)=90°+β,∠COF=∠AOF+∠AOC=![]() +β=
+β=![]() (90°+β).
(90°+β).
所以∠BOE=2∠COF.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】为了应对金融危机,节俭开支,我区某康庄工程指挥部,要对某路段建设工程进行招标,从甲、乙两个工程队的投标书中得知:每天需支付甲队的工程款1.5万元,乙队的工程款1.1万元.甲、乙两个工程队实际施工方案如下:
(1)甲队单独完成这项工程刚好能够如期完成;
(2)乙队单独完成这项工程要比规定的时间多用10天;
(3)若甲、乙两队合作8天,余下的由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.
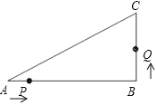
(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个长方形运动场被分隔成A,B,A,B,C共5个区,A区是边长为a m的正方形,C区是边长为c m的正方形.
(1)列式表示每个B区长方形场地的周长,并将式子化简;
(2)列式表示整个长方形运动场的周长,并将式子化简;
(3)如果a=40,c=10,求整个长方形运动场的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
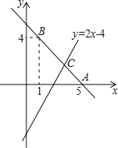
【题目】已知直线y=kx+b经过点A(5,0),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4>kx+b的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com