
分析 由$\sqrt{16}$<$\sqrt{17}$<$\sqrt{25}$,可得出$\sqrt{17}$的整数部分是4;由$\root{3}{64}$<$\root{3}{85}$<$\root{3}{125}$,可得出$\root{3}{85}$的小时部分是$\root{3}{85}$-4.此题得解.
解答 解:∵$\sqrt{16}$<$\sqrt{17}$<$\sqrt{25}$,
∴4<$\sqrt{17}$<5,
∴$\sqrt{17}$在4和5之间.
∴$\sqrt{17}$的整数部分是4.
∵$\root{3}{64}$<$\root{3}{85}$<$\root{3}{125}$,
∴4<$\root{3}{85}$<5,
∴$\root{3}{85}$在4和5之间.
∴$\root{3}{85}$的小时部分是$\root{3}{85}$-4.
故答案为:4;$\root{3}{85}$-4.
点评 本题考查了估计无理数的大小,找出$\sqrt{17}$在4和5之间以及$\root{3}{85}$在4和5之间是解题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:选择题
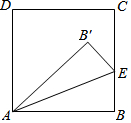 如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )
如图,将正方形ABCD的一角折叠,折痕为AE,∠B′AD比∠B′AE大48°,设∠B′AE和∠B′AD的度数分别为x、y,那么x、y所适合的一个方程组是( )| A. | $\left\{\begin{array}{l}y-x=48\\ y+x=90\end{array}\right.$ | B. | $\left\{\begin{array}{l}y-x=48\\ y=2x\end{array}\right.$ | C. | $\left\{\begin{array}{l}y-x=48\\ y+2x=90\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-y=48\\ y+2x=90\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
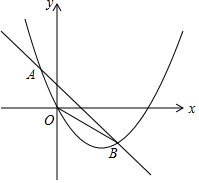 如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,
如图,在平面直角坐标系中,抛物线y=x2-bx与直线交于点A(-$\frac{1}{2}$,m),B(1,n),其中m>0,n<0,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com