
分析 (1)若一元二次方程有两个实数根,则根的判别式△=b2-4ac≥0,建立关于k的不等式,求出k的取值范围.还要注意二次项系数不为0;
(2)设方程的两个为x1,x2,利用两根关系,得出x1+x2=$\frac{2(k-1)}{k-2}$,x1x2=$\frac{k+1}{k-2}$,进一步由它们的倒数和为4,建立关于k的方程,求出k即可.
解答 解:(1)∵方程有两个实数根,
∴根的判别式△=b2-4ac=[-2(k-1)]2-4(k-2)(k+1)=-4k+12≥0,
则k≤3,且k-2≠0,k≠2.
∴k≤3,k≠2.
(2)设方程的两个为x1,x2,
∵x1+x2=$\frac{2(k-1)}{k-2}$,x1x2=$\frac{k+1}{k-2}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{2(k-1)}{k+1}$=4,
解得:k=-3.
点评 本题考查了一元二次方程根的判别式与根与系数的关系的应用.切记不要忽略一元二次方程二次项系数不为零这一隐含条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
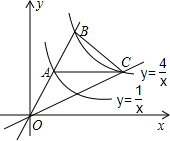 如图,过原点的直线交y=$\frac{4}{x}$,y=$\frac{1}{x}$于B,A两点,AC∥x轴交y=$\frac{4}{x}$于C点,连接OC,则S△OBC=3.
如图,过原点的直线交y=$\frac{4}{x}$,y=$\frac{1}{x}$于B,A两点,AC∥x轴交y=$\frac{4}{x}$于C点,连接OC,则S△OBC=3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com