
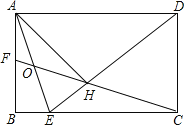
【题目】如图,在矩形ABCD中,![]() ,
,![]() 的平分线交边BC于点E,
的平分线交边BC于点E,![]() 于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:
![]() ,
,![]() ,其中正确命题的序号
,其中正确命题的序号![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
(1)根据矩形的性质得到AD=BC=![]() AB=
AB=![]() CD,由DE平分∠ADC,得到△ADH是等腰直角三角形,△DEC是等腰直角三角形,得到DE=
CD,由DE平分∠ADC,得到△ADH是等腰直角三角形,△DEC是等腰直角三角形,得到DE=![]() CD,得到等腰三角形DAE,求出∠AED=67.5°,∠AEB=67.5°,得到(1)正确;
CD,得到等腰三角形DAE,求出∠AED=67.5°,∠AEB=67.5°,得到(1)正确;
(2)设DH=1,则AH=DH=1,AD=DE=![]() ,求出HE=
,求出HE=![]() ﹣1,得到2
﹣1,得到2![]() HE≠1,所以(2)不正确;
HE≠1,所以(2)不正确;
(3)通过角的度数求出△AOH和△OEH是等腰三角形,从而得到(3)正确;
(4)由△AFH≌△CHE,到AF=EH,由△ABE≌△AHE,得到BE=EH,于是得到BC﹣BF=(BE+CE)﹣(AB﹣AF)=(CD+EH)﹣(CD﹣EH)=2EH,从而得到(4)不正确.
(1)在矩形ABCD中,AD=BC=![]() AB=
AB=![]() CD,∠ADC=∠BCD=90°.
CD,∠ADC=∠BCD=90°.
∵DE平分∠ADC,∴∠ADE=∠CDE=45°.
∵AH⊥DE,∴△ADH是等腰直角三角形,∴AD=![]() AH,∴AH=AB=CD.
AH,∴AH=AB=CD.
∵△DEC是等腰直角三角形,∴DE=![]() CD,∴AD=DE,∴∠AED=67.5°,∴∠AEB=180°﹣45°﹣67.5°=67.5°,∴∠AEH=∠AEB,所以(1)结论正确;
CD,∴AD=DE,∴∠AED=67.5°,∴∠AEB=180°﹣45°﹣67.5°=67.5°,∴∠AEH=∠AEB,所以(1)结论正确;
(2)设DH=1,则AH=DH=1,AD=DE=![]() ,∴HE=DE﹣DH=
,∴HE=DE﹣DH=![]() ﹣1,∴2
﹣1,∴2![]() HE=2
HE=2![]() (
(![]() ﹣1)=4﹣2
﹣1)=4﹣2![]() ≠1,所以(2)结论不正确;
≠1,所以(2)结论不正确;
(3)∵∠AEH=67.5°,∴∠EAH=22.5°.
∵DH=CD,∠EDC=45°,∴∠DHC=67.5°,∴∠OHA=180°﹣90°﹣67.5°=22.5°,∴∠OAH=∠OHA=22.5°,∴OA=OH,∴∠AEH=∠OHE=67.5°,∴OH=OE=OA,∴OH=![]() AE,所以(3)正确;
AE,所以(3)正确;
(4)∵AH=DH,CD=CE.在△AFH与△CHE中,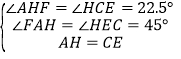 ,∴△AFH≌△CHE,∴AF=EH.在Rt△ABE与Rt△AHE中,
,∴△AFH≌△CHE,∴AF=EH.在Rt△ABE与Rt△AHE中,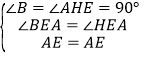 ,∴△ABE≌△AHE,∴BE=EH,∴BC﹣BF=(BE+CE)﹣(AB﹣AF)=(CD+EH)﹣(CD﹣EH)=2EH,所以(4)不正确.
,∴△ABE≌△AHE,∴BE=EH,∴BC﹣BF=(BE+CE)﹣(AB﹣AF)=(CD+EH)﹣(CD﹣EH)=2EH,所以(4)不正确.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度.他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为1:![]() (即AB:BC=1:
(即AB:BC=1:![]() ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为12cm,点P、Q分别是边BC、CA上的动点,点P、Q分别从顶点B、C同时出发,且它们的速度都为3cm/s.
(1)如图1,连接PQ,求经过多少秒后,△PCQ是直角三角形;
(2)如图2,连接AP、BQ交于点M,在点P、Q运动的过程中,∠AMQ的大小是否变化?若变化,请说明理由;若不变,请求出它的度数.
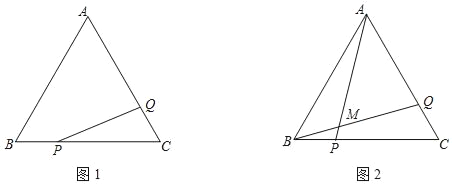
查看答案和解析>>
科目:初中数学 来源: 题型:
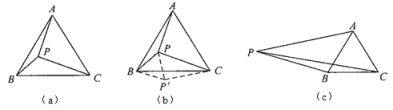
【题目】阅读下列材料:
问题:如图(a)所示,已知点![]() 为等边
为等边![]() 内一点,且
内一点,且![]() ,试探究线段
,试探究线段![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
明明同学的想法是:问题中的线段比较分散,可以通过旋转变换将分散的线段集中在一起,从而解决问题.于是他将![]() 绕点
绕点![]() 顺时针旋转60°,得到了
顺时针旋转60°,得到了![]() ,然后连接
,然后连接![]() .
.
请你参考明明同学的思路,解决下列问题:
(1)图(b)中的![]() 、
、![]() 、
、![]() 之间的数量关系为______.
之间的数量关系为______.
(2)如图(c)所示,点![]() 在等边
在等边![]() 的外部(在直线
的外部(在直线![]() 左侧),满足
左侧),满足![]() ,(1)中的结论仍成立吗?说明你的理由.
,(1)中的结论仍成立吗?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
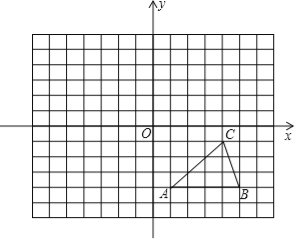
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
(2)以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把直角三角形纸片沿过顶点B的直线(BE交CA于E)折叠,直角顶点C落在斜边AB上,如果折叠后得等腰△EBA,那么结论中:①∠A=30°;②点C与AB的中点重合;③点E到AB的距离等于CE的长,正确的个数是( )
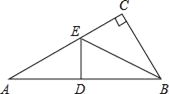
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.
(1)试用树形图或列表法中的一种列举出这两辆汽车行驶方向所有可能的结果;并计算两辆汽车都不直行的概率.
(2)求至少有一辆汽车向左转的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
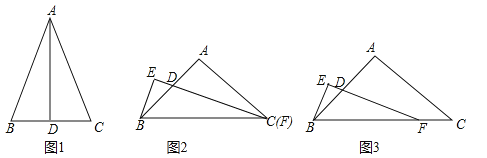
【题目】某中学八年级学生在学习等腰三角形的相关知识时时,经历了以下学习过程:
(1)(探究发现)如图1,在![]() 中,若
中,若![]() 平分
平分![]() ,
,![]() 时,可以得出
时,可以得出![]() ,
,![]() 为
为![]() 中点,请用所学知识证明此结论.
中点,请用所学知识证明此结论.
(2)(学以致用)如果![]() 和等腰
和等腰![]() 有一个公共的顶点
有一个公共的顶点![]() ,如图2,若顶点
,如图2,若顶点![]() 与顶点
与顶点![]() 也重合,且
也重合,且![]() ,试探究线段
,试探究线段![]() 和
和![]() 的数量关系,并证明.
的数量关系,并证明.
(3)(拓展应用)如图3,在(2)的前提下,若顶点![]() 与顶点
与顶点![]() 不重合,
不重合,![]() ,(2)中的结论还成立吗?证明你的结论
,(2)中的结论还成立吗?证明你的结论
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,甲、乙两名大学生骑自行车去距学校6000米的净月潭公园.两人同时从学校出发,以a米/分的速度匀速行驶出发4.5分钟时,甲同学发现忘记带学生证,以1.5a米/分的速度按原路返回学校,取完学生证(在学校取学生证所用时间忽略不计),继续以返回时的速度追赶乙.甲追上乙后,两人以相同的速度前往净月潭.乙骑自行车的速度始终不变.设甲、乙两名大学生距学校的路程为s(米),乙同学行驶的时间为t(分),s与t之间的函数图象如图所示.
(1)求a、b的值.
(2)求甲追上乙时,距学校的路程.
(3)当两人相距500米时,直接写出t的值是_______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com