
 如图,△ABC中,AD∥BC,连接CD交AB于E,且AE:EB=1:3,过E作EF∥BC,交AC于F,S△ADE=2cm2,求S△BCE,S△AEF.
如图,△ABC中,AD∥BC,连接CD交AB于E,且AE:EB=1:3,过E作EF∥BC,交AC于F,S△ADE=2cm2,求S△BCE,S△AEF. 分析 如图,由△ADE∽△BCE,求出△BCE的面积,进而求出△AEC、△ABC的面积;由△AEF∽△ABC,求出△AEF的面积即可解决问题.
解答 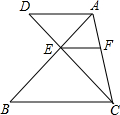 解:如图,
解:如图,
设△ADE、△BCE、△ACE、△ABC、△AEF的面积分别为;
λ、μ、γ、ρ、θ.
∵EF∥BC∥AD,
∴△ADE∽△BCE,
∴$\frac{λ}{μ}$=($\frac{AE}{BE}$)2,而λ=2cm2,AE:EB=1:3,
∴μ=18cm2,即S△BCE=18;
∵γ:μ=AE:BE=1:3,
∴γ=6,△ABC的面积ρ=6+18=24,
∵EF∥BC,
∴△AEF∽△ABC,
∴$\frac{θ}{ρ}$=($\frac{AE}{AB}$)2,而ρ=24,AE:AB=1:4,
∴θ=$\frac{3}{4}$×2=$\frac{3}{2}$,即S△AEF=$\frac{3}{2}$cm2.
综上所述求S△BCE和S△AEF的值分别为18cm2、$\frac{3}{2}$cm2.
点评 该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入把握题意,灵活运用相似三角形的判定及其性质等几何知识点来分析、判断、推理或解答.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
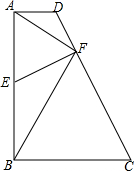 如图,已知四边形ABCD中,AB⊥BC,AD∥BC,E为AB的中点,EF⊥CD于F,且EF=$\frac{1}{2}$AB,连接AF,BF,在不添加辅助线和字母情况下,按要求完成下列各题
如图,已知四边形ABCD中,AB⊥BC,AD∥BC,E为AB的中点,EF⊥CD于F,且EF=$\frac{1}{2}$AB,连接AF,BF,在不添加辅助线和字母情况下,按要求完成下列各题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com