
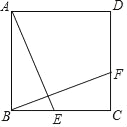
【题目】如图,正方形ABCD中,点E、F分别在边BC和DC上,连接AE、BF,AE⊥BF,点M、N分别在边AB、DC上,连接MN,若MN∥BC,FN=1,BE=2,则BM=_____.
【答案】1或3
【解析】
根据正方形的性质,可得∠ABC与∠C的关系,AB与BC的关系,根据两直线垂直,可得∠AOB的度数,根据同角的余角相等可得∠BAO=∠CBF,根据ASA,可得△ABE≌△BCF,得BE=CF=2,分情况讨论,证明四边形MBCN是平行四边形,则BM=CN,根据两图形可得BM的长.
解:∵四边形ABCD是正方形,
∴∠ABC=∠C=90°,AB=BC.
∵AE⊥BF,
∴∠AOB=∠BAO+∠ABO=90°,
∵∠ABO+∠CBF=90°,
∴∠BAO=∠CBF.
在△ABE和△BCF中,
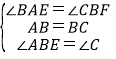 ,
,
∴△ABE≌△BCF(ASA),
∴BE=CF=2,
∵MN∥BC,AB∥CD,
∴四边形MBCN是平行四边形,
∴BM=CN,
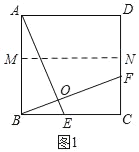
①当N在F的上方时,如图1,
∴BM=CN=CF+FN=2+1=3,
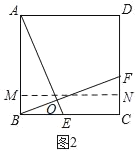
②当N在F的下方时,如图2,
∴BM=CN=CF﹣FN=2﹣1=1,
∴BM的长为1或3,
故答案为:1或3


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4,有下列结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中,正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以BC为直径的⊙O交AC于点E,过点E作AB的垂线交AB于点F,交CB的延长线于点G,且∠ABG=2∠C.
(1)求证:EG是⊙O的切线;
(2)若tanC=![]() ,AC=8,求⊙O的半径.
,AC=8,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如果两个正数a,b,即a>0,b>0,有下面的不等式:![]() ,当且仅当a=b时取到等号我们把
,当且仅当a=b时取到等号我们把![]() 叫做正数a,b的算术平均数,把
叫做正数a,b的算术平均数,把![]() 叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.
叫做正数a,b的几何平均数,于是上述不等式可表述为:两个正数的算术平均数不小于(即大于或等于)它们的几何平均数.它在数学中有广泛的应用,是解决最值问题的有力工具.
初步探究:(1)已知x>0,求函数y=x+![]() 的最小值.
的最小值.
问题迁移:(2)学校准备以围墙一面为斜边,用栅栏围成一个面积为100m2的直角三角形,作为英语角,直角三角形的两直角边各为多少时,所用栅栏最短?
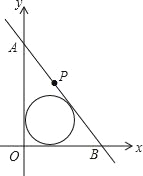
创新应用:(3)如图,在直角坐标系中,直线AB经点P(3,4),与坐标轴正半轴相交于A,B两点,当△AOB的面积最小时,求△AOB的内切圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在![]() 中,
中,![]() 边上的动点
边上的动点![]() 由
由![]() 向
向![]() 运动(与
运动(与![]() ,
,![]() 不重合),点
不重合),点![]() 与点
与点![]() 同时出发,由点
同时出发,由点![]() 沿
沿![]() 的延长线方向运动(
的延长线方向运动(![]() 不与
不与![]() 重合),连结
重合),连结![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是线段
是线段![]() 上一点.
上一点.
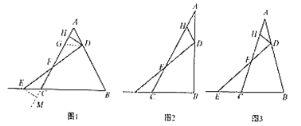
(1)初步尝试:如图,若![]() 是等边三角形,
是等边三角形,![]() ,且点
,且点![]() ,
,![]() 的运动速度相等,求证:
的运动速度相等,求证:![]() .
.
小王同学发现可以由以下两种思路解决此问题:
思路一:过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,先证
,先证![]() ,再证
,再证![]() ,从而证得结论成立;
,从而证得结论成立;
思路二:过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,先证
,先证![]() ,再证
,再证![]() ,从而证得结论成立.
,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分)
(2)类比探究:如图,若在![]() 中,
中,![]() ,
,![]() ,且点
,且点![]() ,
,![]() 的运动速度之比是
的运动速度之比是![]() ,求
,求![]() 的值;
的值;
(3)延伸拓展:如图,若在![]() 中,
中,![]() ,
,![]() ,记
,记![]() ,且点
,且点![]() 、
、![]() 的运动速度相等,试用含
的运动速度相等,试用含![]() 的代数式表示
的代数式表示![]() (直接写出结果,不必写解答过程).
(直接写出结果,不必写解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个红色不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片,在一个蓝色不透明的盒子中放有三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.
(1)从红盒中任意抽取一张红色卡片,从蓝盒中任意抽取一张蓝色卡片,用列举法(树形图或列表法)表示所有的可能情况;
(2)求两张卡片上写有相同数字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 在第一象限内的图象相交于点
在第一象限内的图象相交于点![]() .
.
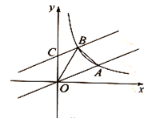
(1)求反比例函数的解析式;
(2)将直线![]() 向上平移后与反比例函数图象在第一象限内交于点
向上平移后与反比例函数图象在第一象限内交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com