
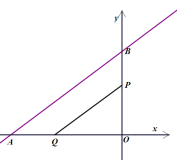
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЕуPДгЕуAГіЗЂЃЌбиелЯпABЉBOЯђжеЕуOдЫЖЏЃЌдкABЩЯвдУПУы5ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌдкBOЩЯвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏ;ЕуQДгЕуOГіЗЂЃЌбиOAЗНЯђвдУПУы
гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЕуPДгЕуAГіЗЂЃЌбиелЯпABЉBOЯђжеЕуOдЫЖЏЃЌдкABЩЯвдУПУы5ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌдкBOЩЯвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏ;ЕуQДгЕуOГіЗЂЃЌбиOAЗНЯђвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏ.PЃЌQСНЕуЭЌЪБГіЗЂЃЌЕБЕуPЭЃжЙЪБЃЌЕуQвВЫцжЎЭЃжЙ.Й§ЕуPзїPEЁЭAOгкЕуEЃЌвдPEЃЌEQЮЊСкБпзїОиаЮPEQFЃЌЩшОиаЮPEQFгыЁїABOжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊS,ЕуPдЫЖЏЕФЪБМфЮЊtУы.
ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏ.PЃЌQСНЕуЭЌЪБГіЗЂЃЌЕБЕуPЭЃжЙЪБЃЌЕуQвВЫцжЎЭЃжЙ.Й§ЕуPзїPEЁЭAOгкЕуEЃЌвдPEЃЌEQЮЊСкБпзїОиаЮPEQFЃЌЩшОиаЮPEQFгыЁїABOжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊS,ЕуPдЫЖЏЕФЪБМфЮЊtУы.
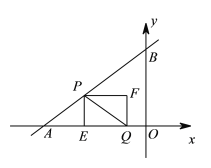
(1)СЌНсPQЃЌЕБPQгыЁїABOЕФвЛБпЦНааЪБЃЌЧѓtЕФжЕ;
(2)ЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪН,ВЂжБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇ.
ЁОД№АИЁПЃЈ1ЃЉЕБ![]() гы
гы![]() ЕФвЛБпЦНааЪБЃЌ
ЕФвЛБпЦНааЪБЃЌ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ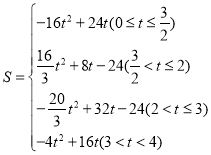
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнвЛДЮКЏЪ§![]() ШЗЖЈЕу
ШЗЖЈЕу![]() ЁЂ
ЁЂ![]() ЕФзјБъЃЌдйгЩ
ЕФзјБъЃЌдйгЩ![]() ЁЂ
ЁЂ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЁЂ
ЁЂ![]() ЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉИљОнЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЁЂЕу
ЩЯЁЂЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЕФЮЛжУВЛЭЌЁЂздБфСП
ЩЯЕФЮЛжУВЛЭЌЁЂздБфСП![]() ЕФЗЖЮЇВЛЭЌЃЌНјааЗжРрЬжТлЃЌЕУГі
ЕФЗЖЮЇВЛЭЌЃЌНјааЗжРрЬжТлЃЌЕУГі![]() гы
гы![]() ЕФЗжЖЮКЏЪ§ЃЎ
ЕФЗжЖЮКЏЪ§ЃЎ
НтЃКЃЈ1ЃЉЁпдк![]() жаЃЌСю
жаЃЌСю![]() ЃЌдђ
ЃЌдђ![]() ЃЛСю
ЃЛСю![]() ЃЌдђ
ЃЌдђ![]()
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]() ЃЌ
ЃЌ![]()
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]()
Ёр
Ёр![]()
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]()
Ёр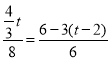
Ёр![]()
ЁрзлЩЯЫљЪіЃЌЕБ![]() гы
гы![]() ЕФвЛБпЦНааЪБЃЌ
ЕФвЛБпЦНааЪБЃЌ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂйЕБ0ЁмtЁм![]() ЪБЃЌжиЕўВПЗжЪЧОиаЮPEQFЃЌШчЭМЃК
ЪБЃЌжиЕўВПЗжЪЧОиаЮPEQFЃЌШчЭМЃК
Ёр![]()
Ёр![]()
Ёр![]()
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
Ёр![]() ЃЛ
ЃЛ
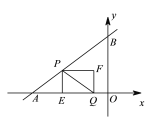
ЂкЕБ![]() ЃМtЁм2ЪБЃЌШчЭМЃЌжиЕўВПЗжЪЧЫФБпаЮPEQMЃЌ
ЃМtЁм2ЪБЃЌШчЭМЃЌжиЕўВПЗжЪЧЫФБпаЮPEQMЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
взЕУ![]()
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
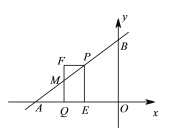
ЂлЕБ2ЃМtЁм3ЪБЃЌжиЕўВПЗжЪЧЮхБпаЮMNPOQЃЌШчЭМЃК
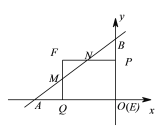
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЂмЕБ3ЃМtЃМ4ЪБЃЌжиЕўВПЗжЪЧОиаЮPOQFЃЌШчЭМЃК
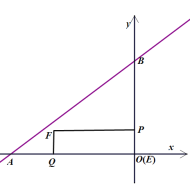
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрзлЩЯЫљЪіЃЌ  ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
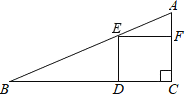
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЃЌAB=10ЃЌAC=6ЃЌЕуEЁЂFЗжБ№ЪЧБпACЁЂBCЩЯЕФЖЏЕуЃЌЙ§ЕуEзїEDЁЭABгкЕуDЃЌЙ§ЕуFзїFGЁЭABгкЕуGЃЌDGЕФГЄЪМжеЮЊ2ЃЎ
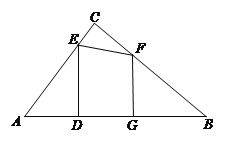
ЃЈ1ЃЉЕБAD=3ЪБЃЌЧѓDEЕФГЄЃЛ
ЃЈ2ЃЉЕБЕуEЁЂFдкБпACЁЂBCЩЯвЦЖЏЪБЃЌЩш![]() ЃЌЧѓyЙигкxЕФКЏЪ§НтЮіЪНЃЌВЂаДГіКЏЪ§ЕФЖЈвхгђЃЛ
ЃЌЧѓyЙигкxЕФКЏЪ§НтЮіЪНЃЌВЂаДГіКЏЪ§ЕФЖЈвхгђЃЛ
ЃЈ3ЃЉ дкЕуEЁЂFвЦЖЏЙ§ГЬжаЃЌЁїAEDгыЁїCEFФмЗёЯрЫЦЃЌШєФмЃЌЧѓADЕФГЄЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдквЛПщаББпГЄ30cmЕФжБНЧШ§НЧаЮФОАхЃЈRtЁїACBЃЉЩЯНиШЁвЛИіе§ЗНаЮCDEFЃЌЕуDдкБпBCЩЯЃЌЕуEдкаББпABЩЯЃЌЕуFдкБпACЩЯЃЌШєAFЃКACЃН1ЃК3ЃЌдђетПщФОАхНиШЁе§ЗНаЮCDEFКѓЃЌЪЃгрВПЗжЕФУцЛ§ЮЊ( )
A. 100cm2B. 150cm2C. 170cm2D. 200cm2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНтЗНГЬ
ЃЈ1ЃЉ![]() ЃЈжБНгПЊЗНЗЈЃЉ
ЃЈжБНгПЊЗНЗЈЃЉ
ЃЈ2ЃЉ![]() ЃЈХфЗНЗЈЃЉ
ЃЈХфЗНЗЈЃЉ
ЃЈ3ЃЉ![]() ЃЈЙЋЪНЗЈЃЉ
ЃЈЙЋЪНЗЈЃЉ
ЃЈ4ЃЉ![]() ЃЈвђЪНЗжНтЗЈЃЉ
ЃЈвђЪНЗжНтЗЈЃЉ
ЃЈ5ЃЉ![]()
ЃЈ6ЃЉ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
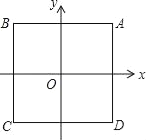
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуOЪЧБпГЄЮЊ2ЕФе§ЗНаЮABCDЕФжааФЃЎКЏЪ§yЃНЃЈxЉhЃЉ2ЕФЭМЯѓгые§ЗНаЮABCDгаЙЋЙВЕуЃЌдђhЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(жаПМЁЄАВЛе)ШчЭМЃЌвбжЊЗДБШР§КЏЪ§yЃН![]() гывЛДЮКЏЪ§yЃНk2xЃЋbЕФЭМЯѓНЛгкA(1ЃЌ8)ЃЌB(Ѓ4ЃЌm)ЃЎ
гывЛДЮКЏЪ§yЃНk2xЃЋbЕФЭМЯѓНЛгкA(1ЃЌ8)ЃЌB(Ѓ4ЃЌm)ЃЎ

(1)Чѓk1ЃЌk2ЃЌbЕФжЕЃЛ
(2)ЧѓЁїAOBЕФУцЛ§ЃЛ
(3)ШєM(x1ЃЌy1)ЃЌN(x2ЃЌy2)ЪЧЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЩЯЕФСНЕуЃЌЧвx1<x2ЃЌy1<y2ЃЌжИГіЕуMЃЌNЮЛгкФФИіЯѓЯоЃЌВЂМђвЊЫЕУїРэгЩЃЎ
ЕФЭМЯѓЩЯЕФСНЕуЃЌЧвx1<x2ЃЌy1<y2ЃЌжИГіЕуMЃЌNЮЛгкФФИіЯѓЯоЃЌВЂМђвЊЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
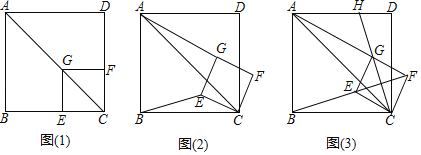
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌвбжЊЕу![]() дкжЙЗНаЮ
дкжЙЗНаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌ
ЃЌ![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЪЧе§ЗНаЮВЂжБНгаДГі
ЪЧе§ЗНаЮВЂжБНгаДГі![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ2ЃЉНЋе§ЗНаЮ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыЗНЯђа§зЊ
ЫГЪБеыЗНЯђа§зЊ![]() ЃЌШчЭМЃЈ2ЃЉЫљаЁЃЌЪдЬНОП
ЃЌШчЭМЃЈ2ЃЉЫљаЁЃЌЪдЬНОП![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉе§ЗНаЮ![]() дка§зЊЙ§ГЬжаЃЌЕБ
дка§зЊЙ§ГЬжаЃЌЕБ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌШ§ЕудквЛЬѕжБЯпЩЯЪБЃЌШчЭМЃЈ3ЃЉЫљЪОЃЌбгГЄ
ЃЌШ§ЕудквЛЬѕжБЯпЩЯЪБЃЌШчЭМЃЈ3ЃЉЫљЪОЃЌбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎШє
ЃЎШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁѕABCDЕФЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌEЪЧвдAЮЊдВаФЃЌвд2ЮЊАыОЖЕФдВЩЯвЛ ЖЏЕуЃЌСЌНсCEЃЌЕуPЮЊCEЕФжаЕуЃЌСЌНсBPЃЌШєAC=![]() ЃЌBD=
ЃЌBD=![]() ЃЌдђBPЕФзюДѓжЕЮЊЃЈ ЃЉ
ЃЌдђBPЕФзюДѓжЕЮЊЃЈ ЃЉ

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЧѓСНЮЛЪ§ЕФЦНЗНЪБЃЌПЩвдгУЭъШЋЦНЗНЪНМАЁАСаЪњЪНЁБЕФЗНЗЈНјааЫйЫуЃЌЧѓНтЙ§ГЬШчЯТЃЎ
Р§ШчЃКЧѓ322ЃЎ
НтЃКвђЮЊ(3xЃЋ2y)2ЃН9x2ЃЋ4y2ЃЋ12xyЃЌНЋЩЯЪНжаЕШКХгвБпЕФЯЕЪ§ЬюШыЯТУцЕФБэИёжаПЩЕУЃК
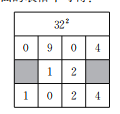
Ыљвд322ЃН1024ЃЎ
(1)ЯТУцЪЧМЮМЮЗТееР§ЬтЧѓ892ЕФвЛВПЗжЙ§ГЬЃЌЧыФуАяЫћЬюШЋБэИёМАзюКѓНсЙћЃЛ
НтЃКвђЮЊ(8xЃЋ9y)2ЃН64x2ЃЋ81y2ЃЋ144xyЃЌНЋЩЯЪНжаЕШКХгвБпЕФЯЕЪ§ЬюШыЯТУцЕФБэИёжаПЩЕУЃК
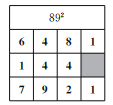
Ыљвд892ЃН ЃЛ
(2)ЗТееР§ЬтЃЌЫйЫу672ЃЛ
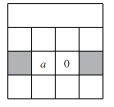
(3)чїчїгУЁАСаЪњЪНЁБЕФЗНЗЈМЦЫувЛИіСНЮЛЪ§ЕФЦНЗНЃЌВПЗжЙ§ГЬШчЭМЫљЪОЃЎШєетИіСНЮЛЪ§ЕФИіЮЛЪ§зжЮЊaЃЌдђетИіСНЮЛЪ§ЮЊ (гУКЌaЕФДњЪ§ЪНБэЪО)ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com