【题目】解方程：
(1)
； (2)
；
(3)2x2－6x－1＝0. (4)2y(y＋2)－y＝2.
【答案】(1) 
； (2) 
；(3) x1＝
，x2＝
；（4）y1＝－2，y2＝
.
【解析】
（1）直接开平方法解解一元二次方程；
（2）（3）使用公式法解一元二次方程；
（4）使用因式分解法解一元二次方程；
（1）
，
解：
，
x2=9,
即
（2）
解：x 2+4x-2=0
a＝1，b＝4，c＝-2，
Δ＝b2－4ac＝42－4×1×(-2)＝24.
∴x=
=
=-2
(3)2x2－6x－1＝0；
解：a＝2，b＝－6，c＝－1，
Δ＝b2－4ac＝(－6)2－4×2×(－1)＝44.
∴x＝
.
∴x1＝，x2＝
.
(4)2y(y＋2)－y＝2.
解：2y(y＋2)－y－2＝0.
2y(y＋2)－(y＋2)＝0.
(y＋2)(2y－1)＝0.
∴y1＝－2，y2＝.
科目：初中数学 来源： 题型：
【题目】定义：在平面直角坐标系中，图形G上点P(x，y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”，记作Zp，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”．
(1)①点A(3，1)的“坐标差”为_______；
②抛物线y＝﹣x2+5x的“特征值”为________；
(2)某二次函数y＝﹣x2+bx+c(c≠0)的“特征值”为﹣1，点B(m，0)与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等．
①直接写出m＝______；(用含c的式子表示)
②求此二次函数的表达式．
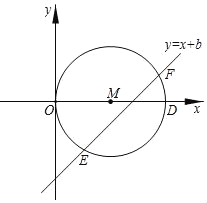
(3)如图，在平面直角坐标系xOy中，点D(4，0)，以OD为直径作⊙M，直线y＝x+b与⊙M相交于点E、F．
①比较点E、F的“坐标差”ZE、ZF的大小．
②请直接写出⊙M的“特征值”为_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
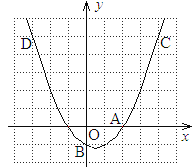
【题目】如图，已知二次函数
的图象过A（2，0），B（0，-1）和C（4，5）三点。
（1）求二次函数的解析式；
（2）设二次函数的图象与
轴的另一个交点为D，求点D的坐标；
（3）在同一坐标系中画出直线
，并写出当在什么范围内时，一次函数的值大于二次函数的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
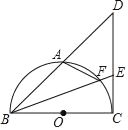
【题目】如图，BC为⊙O的直径，点A是弧BC的中点，连接BA并延长至点D，使得AD＝AB，连接CD，点E为CD上一点，连接BE交弧BC于点F，连接AF．
（1）求证：CD为⊙O的切线；
（2）求证：∠DAF＝∠BEC；
（3）若DE＝2CE＝4，求AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于钝角α，定义它的三角函数值如下：sinα＝sin (180°－α)，cosα＝－cos (180°－α)；若一个三角形的三个内角的比是1∶1∶4，A，B是这个三角形的两个顶点，sinA，cosB是方程4x2－mx－1＝0的两个不相等的实数根，求m的值及∠A和∠B的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列说法不正确的是( )
A. 以等腰三角形顶角的顶点为圆心，底边上的高为半径的圆与底边相切
B. 若两个三角形的边长为8、6、4和4
、3、2，则这两个三角形相似
C. 梯形的中位线平行于两底，并且等于两底和的一半
D. 命题“两圆外离，则两圆无公共点”的逆命题是真命题
查看答案和解析>>
科目：初中数学 来源： 题型：
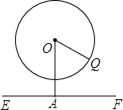
【题目】“五一”节，小雯和同学一起到游乐场玩大型摩天轮，摩天轮的半径为20m，匀速转动一周需要12min，小雯所坐最底部的车厢(离地面0.5m)．
(1)经过2min后小雯到达点Q，如图所示，此时他离地面的高度是多少？
(2)在摩天轮滚动的过程中，小雯将有多长时间连续保持在离地面不低于30.5m的空中？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某小区开展了“行车安全，方便居民”的活动，对地下车库作了改进．如图，这小区原地下车库的入口处有斜坡AC长为13米，它的坡度为i＝1：2.4，AB⊥BC，为了居民行车安全，现将斜坡的坡角改为13°，即∠ADC＝13°（此时点B、C、D在同一直线上）．
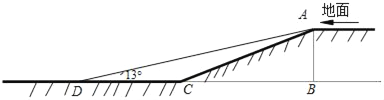
（1）求这个车库的高度AB；
（2）求斜坡改进后的起点D与原起点C的距离（结果精确到0.1米）．
（参考数据：sin13°≈0.225，cos13°≈0.974，tan13°≈0.231，cot13°≈4.331）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
