
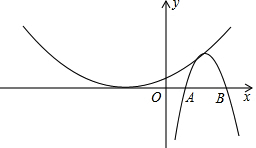 定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.
定义:我们把二次函数y=ax2+bx+c和y=-ax2+bx-c这两个二次函数称为一对友好函数,并称函数y=ax2+bx+c是函数y=-ax2+bx-c的友好函数.函数y=-ax2+bx-c也是函数y=ax2+bx+c的友好函数.分析 (1)任意取一组a、b、c的值代入函数解析式即可得到一对友好函数;
(2)由抛物线的顶点重合可知:$\frac{-b}{-2}=\frac{-b}{2}$,c=-c,从而可求得b=0,c=0;
(3)设点P的坐标为(m,$(\frac{1}{4}m+1)^{2}$),则两抛物线的解析式为y1=$-(x-m)^{2}+(\frac{1}{4}m+1)^{2}$和y2=$(x+m)^{2}-(\frac{1}{4}m+1)^{2}$,然后分别令y1=0,y2=0,从而可解得各点的坐标,从而可求得AB、CD、AD的长度(用含m的式表示),然后根据点D和点A是线段CB的三等分点列出关于m的方程,从而可求得m的值,将m的值代入函数的解析式得到抛物线的一般形式即可求得b、c的值.
解答 解:(1)令a=1,b=2,c=3得:y=ax2+bx+c=x2+2x+3,y=-ax2+bx-c=-x2+2x-3,
∴y=x2+2x+3和y=-x2+2x-3是一对友好函数;
(2)∵两个函数的顶点重合,
∴两抛物线的对称轴重合,即:$\frac{-b}{-2}=\frac{-b}{2}$.
∴b=0.
∴两抛物线的解析式为y=2x2+c和y=-2x2-c.
∵两个函数的顶点重合,
∴c=-c.
解得:c=0,
所以b=0,c=0;
(3)设点P的坐标为(m,$(\frac{1}{4}m+1)^{2}$),则两抛物线的解析式为y1=$-(x-m)^{2}+(\frac{1}{4}m+1)^{2}$和y2=$(x+m)^{2}-(\frac{1}{4}m+1)^{2}$,
令y1=0得:-$(x-m)^{2}+(\frac{1}{4}m+1)^{2}=0$,
解得:xA=$\frac{3}{4}m-1$,xB=$\frac{5}{4}m+1$,
∴AB=$\frac{5}{4}m+1-(\frac{3}{4}m-1)$=$\frac{1}{2}m+2$.
令y2=0得:$(x+m)^{2}-(\frac{1}{4}m+1)^{2}$=0,
解得:xC=$-\frac{5}{4}m-1$,xD=$-\frac{3}{4}m+1$,
如图1: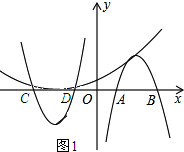
则AD=$\frac{3}{4}m-1-(-\frac{3}{4}m+1)$=$\frac{3}{2}m-2$
∵点D和点A是线段CB的三等分点,
∴AD=AB
∴$\frac{3}{2}m-2=\frac{1}{2}m+2$.
解得:m=4,
∴y1=-(x-4)2+4=-x2+8x-12,所以b=8,c=-12.
如图2;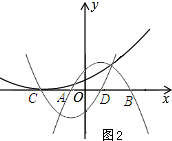
则AD=$-\frac{3}{4}m+1-(\frac{3}{4}m-1)$=2-$\frac{3}{2}m$.
∵点D和点A是线段CB的三等分点,
∴AD=$\frac{1}{2}$AB.
∴$2-\frac{3}{2}m=\frac{1}{2}(\frac{1}{2}m+2)$.
解得:m=$\frac{4}{7}$,
∴y1=$-(x-m)^{2}+(\frac{1}{4}m+1)^{2}$=-$(x-\frac{4}{7})^{2}+(\frac{8}{7})^{2}$=-${x}^{2}+\frac{8}{7}x+\frac{48}{49}$.
∴b=$\frac{8}{7}$,c=$\frac{48}{49}$.
综上所述,可知b=8,c=-12或b=$\frac{8}{7}$,c=$\frac{48}{49}$.
点评 本题主要考查的是二次函数的综合应用,设出点P的坐标,从而得出抛物线的解析式(含字母m),然后求得A、B、C、D各点的横坐标,从而得出AB、AD的长度是解题的关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
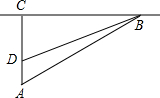 校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载,某中学九年级数学活动小组进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点A,在公路1上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米.已知本路段对校车限速是50千米/时,测得某校车从B到C匀速行驶用时10秒.
校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载,某中学九年级数学活动小组进行了测试汽车速度的实验.如图,先在笔直的公路1旁选取一点A,在公路1上确定点B、C,使得AC⊥l,∠BAC=60°,再在AC上确定点D,使得∠BDC=75°,测得AD=40米.已知本路段对校车限速是50千米/时,测得某校车从B到C匀速行驶用时10秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,抛物线y=x2-4x+3与x轴分别交于A、B两点,交y轴于点C.
如图所示,抛物线y=x2-4x+3与x轴分别交于A、B两点,交y轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{20}{81}$ | B. | $\frac{10}{81}$ | C. | $\frac{5}{243}$ | D. | $\frac{10}{243}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com