
【题目】如图,已知△ABC三个顶点的坐标分别是A(-2,3),B(-3,-1),C(-1,1)
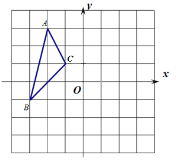
(1)画出△ABC绕点O逆时针旋转90°后的△A1B1C1,并写出点A1的坐标;
(2)画出△ABC绕点O逆时针旋转180°后的△A2B2C2,并写出点A2的坐标;
(3)直接回答:∠AOB与∠A2OB2有什么关系?
【答案】(1)作图见解析,(-4,-2);(2)作图见解析,(2,-3);(3)相等.
【解析】
试题分析:(1)根据旋转的性质作图,写出点的坐标;
根据旋转的性质作图,写出点的坐标;
(3)根据旋转的性质得出结论.
试题解析:(1)作图如下,点A1的坐标(-4,-2).
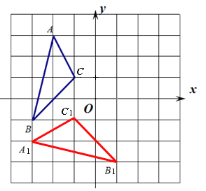
(2)作图如下,点A2的坐标(2,-3).
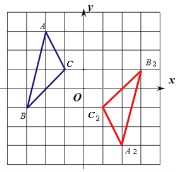
(3)相等.
考点:1.旋转作图;2.旋转的性质.
【题型】解答题
【结束】
20
【题目】已知函数y=(m﹣2)xm2+m-4 +2x﹣1是一个二次函数,求该二次函数的解析式.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“阅读素养的培养是构建核心素养的重要基础,重庆十一中学校以‘大阅读’特色课程实施为突破口,着力提升学生的核心素养.”全校师生积极响应和配合,开展各种活动丰富其课余生活.在数学兴趣小组中,同学们从书上认识了很多有趣的数.其中有一个“和平数”引起了同学们的兴趣.描述如下:一个四位数,记千位上和百位上的数字之和为x,十位上和个位上的数字之和为y,如果![]() ,那么称这个四位数为“和平数”.
,那么称这个四位数为“和平数”.
例如:1423,![]() ,
,![]() ,因为
,因为![]() ,所以1423是“和平数”.
,所以1423是“和平数”.
(1)直接写出:最小的“和平数”是________,最大的“和平数”是__________;
(2)求同时满足下列条件的所有“和平数”:
①个位上的数字是千位上的数字的两倍;
②百位上的数字与十位上的数字之和是12的倍数;
(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后这两个“和平数”为“相关和平数”.
例如:1423于4132为“相关和平数”
求证:任意的两个“相关和平数”之和是1111的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,以
上一动点,以![]() 为边向右侧作等边
为边向右侧作等边![]() ,点
,点![]() 的位置随着点
的位置随着点![]() 的位置变化而变化.
的位置变化而变化.

(1)如图1,当点![]() 在四边形
在四边形![]() 内部或边上时,连接
内部或边上时,连接![]() ,
,![]() 与
与![]() 的数量关系是________,
的数量关系是________,![]() 与
与![]() 的位置关系是_______;
的位置关系是_______;
(2)如图2,当点![]() 在四边形
在四边形![]() 外部时,(1)中的结论是否还成立?若成立,请予以证明;
外部时,(1)中的结论是否还成立?若成立,请予以证明;
(3)如图3,当点![]() 在线段
在线段![]() 的延长线上时,连接
的延长线上时,连接![]() ,若
,若![]() ,
,![]() ,则线段
,则线段![]() ______,
______,![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数分别填在相应的大括号内:25,-0.91,![]() ,3.14,-7,0,-50,
,3.14,-7,0,-50,![]() ,9.
,9.
(1)整数有:{ }; (2)分数有:{ };
(3)正整数有:{ }; (4)负整数有:{ };
(5)正分数有:{ }; (6)负分数有:{ };
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
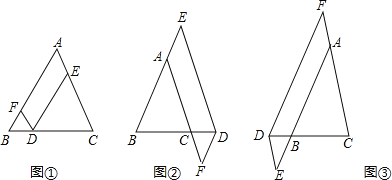
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com