
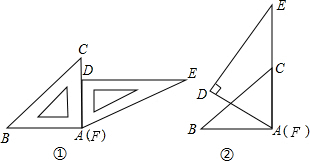
| A. | 6+2$\sqrt{3}$ | B. | 9 | C. | 10 | D. | 6+6$\sqrt{2}$ |
分析 过G点作GH⊥AC于H,由等腰直角三角形的性质得出GH=CH=$\frac{\sqrt{2}}{2}$CG=6cm,再由三角函数求出AH=$\frac{\sqrt{3}}{3}$GH,即可得出AC.
解答 解:过G点作GH⊥AC于H,如图所示:
则∠GAC=60°,∠GCA=45°,GC=6$\sqrt{2}$,
在Rt△GCH中,GH=CH=$\frac{\sqrt{2}}{2}$CG=6,
在Rt△AGH中,AH=$\frac{\sqrt{3}}{3}$GH=2$\sqrt{3}$,
∴AC=CH+AH=6+2$\sqrt{3}$,
故选:A.
点评 本题考查了旋转的性质、解直角三角形,熟练掌握旋转的性质:①对应点到旋转中心的距离相等,②对应点与旋转中心所连线段的夹角等于旋转角,③旋转前、后的图形全等是解题的关键.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:填空题
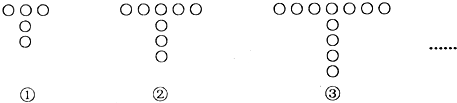
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知△ABC,∠ABC,∠ACB的角平分线交于点O,连接AO并延长交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA长为( )cm.
如图,已知△ABC,∠ABC,∠ACB的角平分线交于点O,连接AO并延长交BC于D,OH⊥BC于H,若∠BAC=60°,OH=3cm,OA长为( )cm.| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=14,b=48,c=49 | B. | a=3,b=5,c=4 | C. | a=9,b=40,c=41 | D. | a=8,b=15,c=17 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
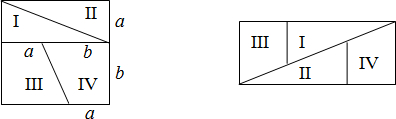
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$+1 | D. | $\sqrt{3}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com