
【题目】若x﹣m与x+3的乘积中不含x的一次项,则m的值为( )
A.3B.1C.0D.﹣3
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,等腰△ ABC 的周长为 21,底边 BC=5,AB 的垂直平分线 DE 交 AB 于点 D,交 AC于点 E,则△BEC 的周长为( )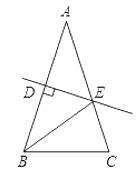
A.13
B.14
C.15
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时50海里的速度向正东方航行,在![]() 处测得灯塔
处测得灯塔![]() 在北偏东
在北偏东![]() 方向上,继续航行1小时到达
方向上,继续航行1小时到达![]() 处,此时测得灯塔
处,此时测得灯塔![]() 在北偏东
在北偏东![]() 方向上.
方向上.
(1)求![]() 的度数;
的度数;
(2)已知在灯塔![]() 的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?
的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题:“P 是等边△ABC 内的一点,若 P 到三边的距离相等,则 PA=PB=PC.”
(1)写出它的逆命题.判断其逆命题成立吗?若成立,请给出证明.
(2)进一步证明:点 P 到等边△ABC 各边的距离之和为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题探究发现
(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
填空:①∠AEB的度数为;②线段AD,BE之间的数量关系为 . 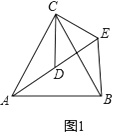
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.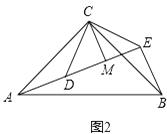
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计:超速行驶是引发交通事故的主要原因,学完第一章后,李鹏、王军、张力三位同学尝试用自己所学的知识检测车速,他们决定在峨城大道金源山水城路段进行测试汽车速度的实验,并把观测点设在到公路l的距离为30米的点P处,选择了一辆匀速行驶的大众轿车作为观测对象,测得此车从A处行驶到B处所用的时间为3秒,并测得∠PAO=45°,同时发现将△BPO沿过A点的直线折叠,点B能与点P重合,试判断此车是否超过了每小时60千米的限制速度?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决中小学大班额问题,东营市各县区今年将改扩建部分中小学,某县计划对A、B两类学校进行改扩建,根据预算,改扩建2所A类学校和3所B类学校共需资金7800万元,改扩建3所A类学校和1所B类学校共需资金5400万元.
(1)改扩建1所A类学校和1所B类学校所需资金分别是多少万元?
(2)该县计划改扩建A、B两类学校共10所,改扩建资金由国家财政和地方财政共同承担.若国家财政拨付资金不超过11800万元;地方财政投入资金不少于4000万元,其中地方财政投入到A、B两类学校的改扩建资金分别为每所300万元和500万元.请问共有哪几种改扩建方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com