
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC=![]() ,以AB为斜边另作Rt△APB,连接PC,当点P在AC左侧时,下列结论正确的是( )
,以AB为斜边另作Rt△APB,连接PC,当点P在AC左侧时,下列结论正确的是( )
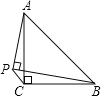
A. ![]() 的度数不确定B.
的度数不确定B. ![]()
C. 当![]() 时,
时,![]() D. 当
D. 当![]() 时,
时,![]()
【答案】D
【解析】
因为∠ACB=∠APB=90°,可得A,P,C,B四点共圆,即∠CPB=∠CAB=45°,可得∠APC=∠APB+∠CPB=90°+45°=135°,故选项A错误;过点C作CP的垂线交PB于点K,证明△BCK≌△ACP,得AP=BK,所以PB=![]() PC+PA,故选项B错误;当PA=1时和PA=PC时,结合PB=
PC+PA,故选项B错误;当PA=1时和PA=PC时,结合PB=![]() PC+PA的关系式,即可对选项C,D作出判断.
PC+PA的关系式,即可对选项C,D作出判断.
解:∵∠ACB=∠APB=90°,
∴A,P,C,B四点共圆,
∵AC=BC,
∴∠CAB=45°,
∴∠CPB=∠CAB=45°,
∴∠APC=∠APB+∠CPB=90°+45°=135°,
∴选项A错误;
如图,过点C作CP的垂线交PB于点K,
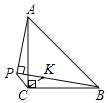
∵∠CPK=45°,
∴∠CKP=∠CPK=45°,
∴PC=KC,∠CKB=∠CPA=135°,
∵∠PCK=∠ACB=90°,
∴∠BCK=∠ACP,
∴△BCK≌△ACP((ASA),
∴AP=BK,
∵PK=![]() PC,
PC,
∴PB=![]() PC+PA,
PC+PA,
∴选项B错误;
当PA=1时,
∵AC=BC=![]() ,
,
∴AB=2,
∴PB=![]() =
=![]() ,
,
∵PB=![]() PC+PA,
PC+PA,
∴![]() =
=![]() PC+1,
PC+1,
解得PC=![]() ,
,
∴选项C错误;
当PA=PC时,
PB=(![]() +1)PA,
+1)PA,
∵PA2+PB2=AB2,
∴(![]() -1)2PB2+PB2=4,
-1)2PB2+PB2=4,
解得PB2=2+![]()
∴选项D正确.
故选:D.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】某学校准备购买若干台电脑和打印机,如果购买![]() 台电脑和
台电脑和![]() 台打印机,一共花费
台打印机,一共花费![]() 元;如果购买
元;如果购买![]() 台电脑和
台电脑和![]() 台打印机,一共花费
台打印机,一共花费![]() 元;
元;
(1)求每台电脑和每台打印机的价格分别是多少元?
(2)如果学校购买电脑和打印机的预算费用不超过![]() 元,并且购买打印机的台数要比购买电脑的台数多
元,并且购买打印机的台数要比购买电脑的台数多![]() 台,那么该学校最多能购买多少台打印机?
台,那么该学校最多能购买多少台打印机?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
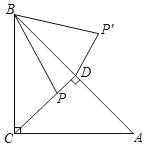
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
查看答案和解析>>
科目:初中数学 来源: 题型:
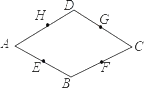
【题目】已知四边形ABCD为菱形,点E、F、G、H分别为各边中点,判断E、F、G、H四点是否在同一个圆上,如果在同一圆上,找到圆心,并证明四点共圆;如果不在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
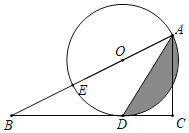
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,点E在AB上,以AE为直径的⊙O经过点D.
(1)求证:直线BC是⊙O的切线;
(2)若∠B=30°,AC=3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三个质地、大小都相同的小球分别标上数字2,-2,3后放入一个不透明的口袋搅匀,任意摸出一个小球,记下数字a后,放回口袋中搅匀,再任意摸出一个小球,又记下数字b.这样就得到一个点的坐标(a,b).
(1)求这个点(a,b)恰好在函数y=-x的图像上的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)
(2)如果再往口袋中增加n(n≥1)个标上数字2的小球,按照同样的操作过程,所得到的点(a,b)恰好在函数y=-x的图像上的概率是 (请用含n的代数式直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于二次函数y=-x2-2x+3说法正确的是( )
A. 当![]() 时,函数最大值4
时,函数最大值4
B. 当![]() 时,函数最大值2
时,函数最大值2
C. 将其图象向上平移3个单位后,图象经过原点
D. 将其图象向左平移3个单位后,图象经过原点
查看答案和解析>>
科目:初中数学 来源: 题型:
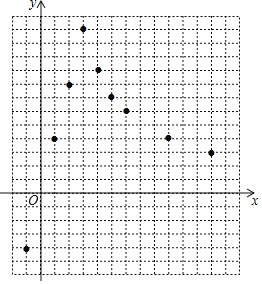
【题目】初三某班同学小戴想根据学习函数的经验,通过研究一个未学过的函数的图象,从而探究其各方面性质.
下表是函数y与自变量x的几组对应值:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 12 | … |
y | … | -4 | 0 | 4 | 8 | 12 | 9 | 7.2 | 6 | 4 | 3 | … |
(1)在平面直角坐标系xOy中,每个小正方形的边长为一个单位长度,描出了以上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象.
(2)请根据画出的函数图象,直接写出该函数的关系式y=______(请写出自变量的取值范围),并写出该函数的一条性质:______.
(3)当直线y=-![]() x+b与该函数图象有3个交点时,求b的取值范围.
x+b与该函数图象有3个交点时,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com