下列关系式正确的是( )A．35.5°=35°5′B．35.5°=35°50′C．35.5°＜35°5′D．35.5°＞35°5′ 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

12．下列关系式正确的是（　　）

A．

35.5°=35°5′

B．

35.5°=35°50′

C．

35.5°＜35°5′

D．

35.5°＞35°5′

分析根据大单位化小单位乘以进率，可得答案．

解答解：A、35.5°=35°30′，35°30′＞35°5′，故A错误；
B、35.5°=35°30′，35°30′＜35°50′，故B错误；
C、35.5°=35°30′，35°30′＞35°5′，故C错误；
D、35.5°=35°30′，35°30′＞35°5′，故D正确；
故选：D．

点评本题考查了度分秒的换算，大单位化成效单位乘以进率是解题关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

2．先化简，再求值：$\frac{{a}^{2}-2ab+{b}^{2}}{2a-2b}$÷（$\frac{1}{b}$-$\frac{1}{a}$），其中a=$\sqrt{5}$，b=2．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

3．

如图，平行四边形ABCD的对角线AC、BD交于点O，若AC=DC=4，BD=6，则△AOB的周长为（　　）

A．

B．

C．

D．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

20．

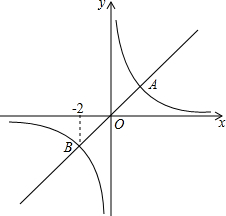正比例函数y₁=k₁x的图象与反比例函数y₂=$\frac{{k}_{2}}{x}$的图象相交于A，B两点，其中点B的横坐标为-2，当y₁＜y₂时，x的取值范围是（　　）

A．

x＜-2或x＞2

B．

x＜-2或0＜x＜2

C．

-2＜x＜0或0＜x＜2

D．

-2＜x＜0或x＞2

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．

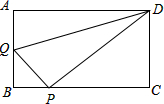在矩形ABCD中，AB=3，AD=4，动点Q从点A出发，以每秒1个单位的速度，沿AB向点B移动；同时点P从点B出发，仍以每秒1个单位的速度，沿BC向点C移动，连接QP，QD，PD．若两个点同时运动的时间为x秒（0＜x≤3），解答下列问题：
（1）设△QPD的面积为S，用含x的函数关系式表示S；当x为何值时，S有最大值？并求出最小值；
（2）是否存在x的值，使得QP⊥DP？试说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

17．一组数据2，4，a，7，7的平均数$\overline{x}$=5，则方差S²=3.6．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

2．

如图，已知O是直线MN上的一点，∠AOB=90°，经过点O的直线DC平分∠BON，∠1=38°，求∠3和∠DOA的度数．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

19．（1）计算：（$\frac{1}{2}$-$\frac{5}{9}$+$\frac{7}{12}$）×（-36）
（2）计算：100÷（-2）²-（-2）÷（-$\frac{2}{3}$）
（3）化简：（-x²+3xy-$\frac{1}{2}{y}^{2}$）-（-$\frac{1}{2}$x²+4xy-$\frac{3}{2}$y²）
（4）先化简后求值：x²+（2xy-3y²）-2（x²+yx-2y²），其中x=-$\frac{1}{2}$，y=3．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．

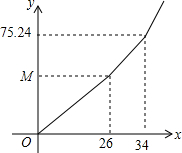某市为鼓励居民节约用水，实行新的阶梯水价，即按用水量进行分段收费，阶段水价方案主要分为三档：
第一档每户每月的基准水量为26立方米，在此之内的用水量（含26立方米），按1.98元/立方米计收水费；
第二档用水量的基数为26-34立方米（即超过26立方米，但不超过34立方米），这部分水费按2.97元/立方米计收水费；
第三档每月超过34立方米以上部分的水费，按3.96元/立方米的标准计收水费．
图中折线反映的是实行阶梯水价后每月收取水费y（元）与用水量x（立方米）之间的函数关系．
（1）写出M点的坐标（26，51.48）；
（2）当x＞34时，求y与x之间的函数关系式；
（3）市民刘阿姨家是一个四口之家，由于七月天气较热，刘阿姨家用水较多，七月份的水费为99元，问刘阿姨家七月份用水多少立方米？

查看答案和解析>>

同步练习册答案