
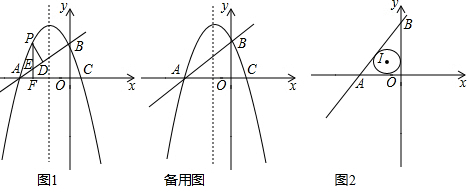
ЗжЮі ЃЈ1ЃЉАбЕуAЁЂBЁЂCЕФзјБъДњШыХзЮяЯпНтЮіЪНЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪННтД№МДПЩЃЛ
ЃЈ2ЃЉИљОнЕуAЁЂBЕФзјБъЧѓГіOA=OBЃЌДгЖјЕУЕНЁїAOBЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУЁЯBAO=45ЁуЃЌШЛКѓЧѓГіЁїPEDЪЧЕШбќжБНЧШ§НЧаЮЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪЃЌPDдНДѓЃЌЁїPDEЕФжмГЄзюДѓЃЌдйХаЖЯГіЕБгыжБЯпABЦНааЕФжБЯпгыХзЮяЯпжЛгавЛИіНЛЕуЪБЃЌPDзюДѓЃЌдйЧѓГіжБЯпABЕФНтЮіЪНЮЊy=x+3ЃЌЩшгыABЦНааЕФжБЯпНтЮіЪНЮЊy=x+mЃЌгыХзЮяЯпНтЮіЪНСЊСЂЯћЕєyЃЌЕУЕНЙигкxЕФвЛдЊЖўДЮЗНГЬЃЌРћгУИљЕФХаБ№ЪНЁї=0СаЪНЧѓГіmЕФжЕЃЌдйЧѓГіxЁЂyЕФжЕЃЌДгЖјЕУЕНЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЂйШчЭМ2ЃЌЕуMдкЖдГЦжсЩЯЪБЃЌЙ§ЕуPзїPQЁЭЖдГЦжсгкQЃЌРћгУЯрЫЦШ§НЧаЮаджЪМДПЩЧѓГіЕуPзјБъЃЌЂкШчЭМ3жаЃЌЕуNдкЖдГЦжсЩЯЪБЃЌЩшХзЮяЯпЖдГЦжсгыxжсНЛгкЕуQЃЌРћгУЯрЫЦШ§НЧаЮаджЪЧѓГіPFЃЌМДПЩХаЖЯдйдкетжжЧщаЮВЛКЯЬтвтЃЎЂлШчЭМ3-1жаЃЌЭЌЗЈПЩЧѓЃЎ
ЃЈ4ЃЉШчЭМ4жаЃЌЙ§ЕуQзїЁбIЕФЧаЯпQMЃЌЕуQЁфзїЁбIЕФЧаЯпQЁфNЃЌЯШЧѓГіФкЧадВЕФАыОЖЃЌдйЧѓГіЕБЁЯMDQ=60ЁуЪБЃЌDQЕФГЄЃЌдйИљОнЖдГЦадМДПЩНтОіЮЪЬтЃЎ
НтД№ НтЃКЃЈ1ЃЉАбAЃЈ-3ЃЌ0ЃЉЁЂCЃЈ1ЃЌ0ЃЉДњШыy=ax2+bx+3
ЕУ$\left\{\begin{array}{l}{9a-3b+3=0}\\{a+b+3=0}\end{array}\right.$НтЕУ$\left\{\begin{array}{l}{a=-1}\\{b=-2}\end{array}\right.$ЃЌ
ЁрХзЮяЯпНтЮіЪНЮЊy=-x2-2x+3ЃЎ
ЃЈ2ЃЉШчЭМ1жаЃЌЁпAЃЈ-3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌ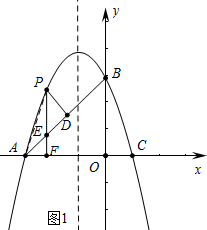
ЁрOA=OB=3ЃЌ
ЁрЁїAOBЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрЁЯBAO=45ЁуЃЌ
ЁпPFЁЭxжсЃЌ
ЁрЁЯAEF=90Ёу-45Ёу=45ЁуЃЌ
гжЁпPDЁЭABЃЌ
ЁрЁїPDEЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрPDдНДѓЃЌЁїPDEЕФжмГЄдНДѓЃЌ
взЕУжБЯпABЕФНтЮіЪНЮЊy=x+3ЃЌ
ЩшгыABЦНааЕФжБЯпНтЮіЪНЮЊy=x+mЃЌ
СЊСЂ$\left\{\begin{array}{l}{y=x+m}\\{y=-{x}^{2}-2x+3}\end{array}\right.$ЃЌ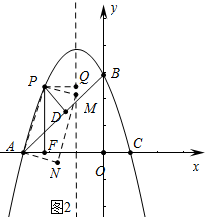
ЯћЕєyЕУЃЌx2+3x+m-3=0ЃЌ
ЕБЁї=32-4ЁС1ЁСЃЈm-3ЃЉ=0ЃЌ
МДm=$\frac{21}{4}$ЪБЃЌжБЯпгыХзЮяЯпжЛгавЛИіНЛЕуЃЌPDзюГЄЃЌ
ДЫЪБx=-$\frac{3}{2}$ЃЌy=-$\frac{3}{2}$+$\frac{21}{4}$=$\frac{15}{4}$ЃЌ
ЁрЕуPЃЈ-$\frac{3}{2}$ЃЌ$\frac{15}{4}$ЃЉЪБЃЌЁїPDEЕФжмГЄзюДѓЃЛ
ЃЈ3ЃЉЂйШчЭМ2ЃЌЕуMдкЖдГЦжсЩЯЪБЃЌЙ§ЕуPзїPQЁЭЖдГЦжсгкQЃЌ
дкОиаЮAPMNжаЃЌAP=PMЃЌЁЯAPM=90ЁуЃЌ
ЁрЁЯAPF+ЁЯFPM=90ЁуЃЌЁЯQPM+ЁЯFPM=90ЁуЃЌ
ЁрЁЯAPF=ЁЯQPMЃЌ
ЁрЁїAPFЁзЁїMPQЃЌ
Ёр$\frac{PF}{PQ}$=$\frac{PA}{PM}$=4ЃЌ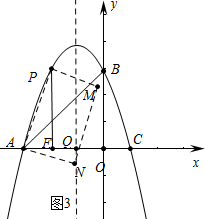
ЩшЕуPЕФКсзјБъЮЊnЃЈnЃМ0ЃЉЃЌдђPQ=-1-nЃЌ
МДPF=-4-4nЃЌ
ЁрЕуPЕФзјБъЮЊЃЈnЃЌ-4-4nЃЉЃЌ
ЁпЕуPдкХзЮяЯпy=-x2-2x+3ЩЯЃЌ
Ёр-n2-2n+3=-4-4nЃЌ
ећРэЕУЃЌn2-2n-7=0ЃЌ
НтЕУn=1-2$\sqrt{2}$Лђ1+2$\sqrt{2}$ЃЈЩсЦњЃЉЃЌ
ЫљвдЃЌЕуPЕФзјБъЮЊЃЈ1-2$\sqrt{2}$ЃЌ-8+8$\sqrt{2}$ЃЉЃЛ
ЂкШчЭМ3жаЃЌЕуNдкЖдГЦжсЩЯЪБЃЌЩшХзЮяЯпЖдГЦжсгыxжсНЛгкЕуQЃЌ
ЁпЁЯPAF+ЁЯFPA=90ЁуЃЌЁЯPAF+ЁЯQAN=90ЁуЃЌ
ЁрЁЯFPA=ЁЯQANЃЌ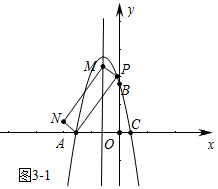
гжЁпЁЯPFA=ЁЯAQN=90ЁуЃЌ
ЁрЁїAPFЁзЁїNAQЃЌ
Ёр$\frac{AP}{AN}$=$\frac{PF}{AQ}$=4ЃЌ
ЁпAQ=2ЃЌ
ЁрPF=8ЃО4ЃЈВЛКЯЬтвтЃЉЃЌ
ЂлШчЭМ3-1жаЃЌЭЌЗЈПЩЧѓPЃЈ-3+2$\sqrt{2}$ЃЌ-8+8$\sqrt{2}$ЃЉ
злЩЯЫљЪіЕуPЕФзјБъЮЊЃЈ1-2$\sqrt{2}$ЃЌ-8+8$\sqrt{2}$ЃЉЛђЃЈ-3+2$\sqrt{2}$ЃЌ-8+8$\sqrt{2}$ЃЉЃЎ
ЃЈ4ЃЉШчЭМ4жаЃЌ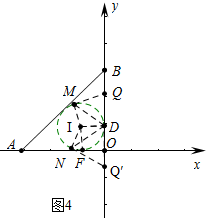 ЁпOA=OB=3ЃЌЁЯAOB=90ЁуЃЌ
ЁпOA=OB=3ЃЌЁЯAOB=90ЁуЃЌ
ЁрAB=3$\sqrt{2}$ЃЌ
ЩшЁбIЗжБ№ЧаOAЁЂOBгкFЁЂDЃЎСЌНгIDЁЂIFЃЎ
дђЫФБпаЮIDOFЪЧе§ЗНаЮЃЌID=$\frac{OA+OB-AB}{2}$=3-$\frac{3}{2}$$\sqrt{2}$ЃЌ
Й§ЕуQзїЁбIЕФЧаЯпQMЃЌЕуQЁфзїЁбIЕФЧаЯпQЁфNЃЌ
ЕБЁЯMDQ=60ЁуЪБЃЌDQ=ID•tan60Ёу=3$\sqrt{3}$-$\frac{3}{2}$$\sqrt{6}$ЃЌ
ЁрOQ=3-$\frac{3}{2}$$\sqrt{2}$+3$\sqrt{3}$-$\frac{3}{2}$$\sqrt{6}$ЃЌ
ИљОнЖдГЦадЕБЁЯNQЁфD=60ЁуЪБЃЌOQЁф=ЃЈ3$\sqrt{3}$-$\frac{3}{2}$$\sqrt{6}$-3+$\frac{3}{2}$$\sqrt{2}$ЃЉЃЌ
ЁрШєЁбIЩЯДцдкСНИіЕуMЃЌNЃЌЪЙЁЯMQN=60ЁуЪБЃЌ3$\sqrt{3}$-$\frac{3}{2}$$\sqrt{6}$-3+$\frac{3}{2}$$\sqrt{2}$ЁмtЁм3-$\frac{3}{2}$$\sqrt{2}$+3$\sqrt{3}$-$\frac{3}{2}$$\sqrt{6}$ЃЎ
ЕуЦР БОЬтЪЧЖўДЮКЏЪ§злКЯЬтаЭЃЌжївЊПМВщСЫД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§НтЮіЪНЃЌЕШбќжБНЧШ§НЧаЮЕФХаЖЈгыаджЪЃЌе§ЗНаЮЕФаджЪЃЌШЋЕШШ§НЧаЮЕФХаЖЈгыаджЪЃЌХзЮяЯпЩЯЕуЕФзјБъЬиеїЃЌЃЈ2ЃЉШЗЖЈГіЁїPDEЪЧЕШбќжБНЧШ§НЧаЮЃЌДгЖјХаЖЯГіЕуPЮЊЦНаагкABЕФжБЯпгыХзЮяЯпжЛгавЛИіНЛЕуЪБЕФЮЛжУЪЧНтЬтЕФЙиМќЃЌЃЈ3ЃЉИљОнШЋЕШШ§НЧаЮЕФаджЪгУЕуPЕФКсзјБъБэЪОГізнзјБъЛђгУзнзјБъЧѓГіКсзјБъЪЧНтЬтЕФЙиМќЃЎЃЈ4ЃЉНтЬтЙиМќЪЧЧѓГіЁЯDQM=60ЁуЪБЃЌDQЕФГЄЃЎЪєгкжаПМбЙжсЬтЃЎ


 ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
ЦкФЉГхДЬ100ЗжДДаТН№ОэЭъШЋЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | 2ЃЈx-1ЃЉ=1-ЃЈ3x+1ЃЉ | BЃЎ | 2ЃЈx-1ЃЉ=6-ЃЈ3x+1ЃЉ | CЃЎ | 2x-1=1-ЃЈ3x+1ЃЉ | DЃЎ | 2ЃЈx-1ЃЉ=6-3x+1 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | aЁн1 | BЃЎ | 1ЃМaЁм2 | CЃЎ | 1ЁмaЃМ2 | DЃЎ | 1ЃМaЃМ2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com